
前回までは体積でしたが、今回は曲線の長さです。次元が下がった?でもメンドウなことは変わりない?「公式」に当てはめていけばMaxima様はいとも容易く解答をご提示くださるのですが、その先、端的に言うと「宿題のお答え」風に整形するのが辛いです。一撃でやってくれる方法ないのかしら。答えは出ているのだから文句いうなと?
※「忘却の微分方程式」投稿順 index はこちら
※数学のお勉強のための以下の教科書(参考書、問題集?)の例題をMaximaの練習に使わせていただいております。
遥かなるかな太古の時代、大学生のときにこういう御本が欲しかったデス。
※以下のMaxima/wxMaximaバージョンで実習させていただいております。
-
- Maxima 5.46.0
- wxMaxima 22.04.0
曲線の弧長の公式
パラメータ表示x=f(t)、 y=g(t)、a≦t≦b の曲線の弧長の公式は以下です。まあ見た通りな感じ。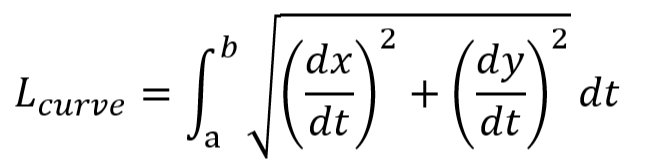
一方、y=f(x)、a≦x≦bという表現であれば、以下です。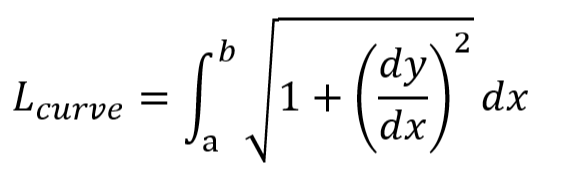
まあ、これが分かっていれば、曲線の長さは自在に求まる?ハズ。
今回の問題
今回の問題をグラフ、2次元の、にしてみました。2次元のグラフ、前回までの3次元のグラフにくらべるとお楽、とってもお楽。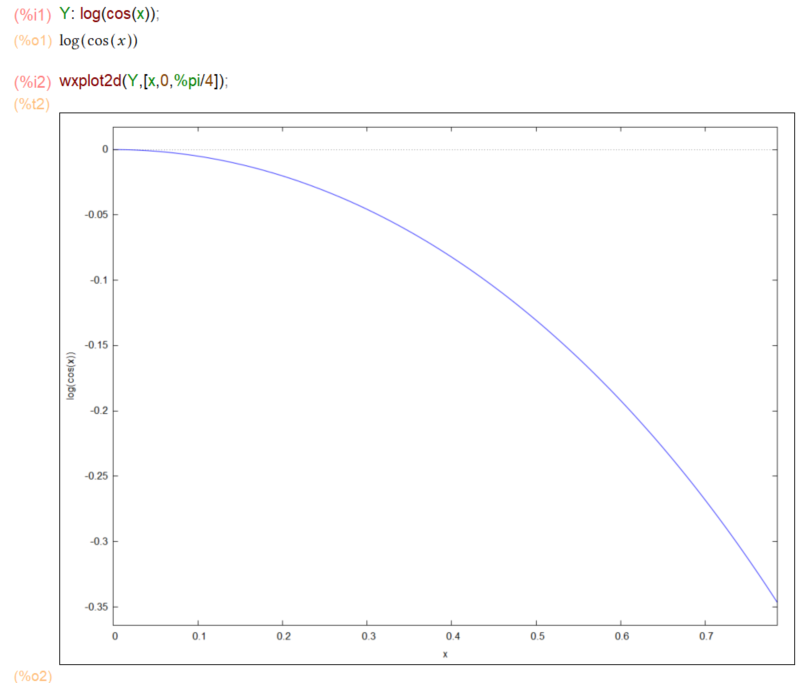
上記のグラフの線分の長さを求めるために公式通りに以下のLを定義しました。積分の中に平方根があり、その中に微分の2乗が入ってますが、なんのそのです(Maxima様にとっては。)
evで定積分を評価するときに、cos(x)は正の数なの?と誰何されましたが指定すればお答えは一発。xは0からπ/4と言っているのだから、そのくらいよきに計らってくれんのかなあ。
上記の黄色のマーカ部がお答えです。ただ、数学の宿題のお答え的にはちと形が悪うございます。外にでているマイナスをlogの内側に引っ込めて、中身を整理(有理化)したいです。
マイナスをLogの内側に引っ込めるやり方がわかりませぬ。引っ込めた値をL1として以下のように定義し、その log をとるとちゃんと元に戻るのでL1が「中の人」であることはOK、多分。
そこで、中の分母分子に1+√2を掛けて、から整理してlogとったものが以下に。
上記の黄色のマーカで、宿題のお答え風にまで変形できましたが、なんだかな~。この辺、一発でできんものなのかなあ。わからん。

