
前回は素朴な方法で2次元配列に乱数を詰め込みました。今回は詰め込んだ配列2つをもってきて行列積を求めてみたいと思います。これまた一目瞭然な素朴な方法。後々いろいろ実験するための準備とな。しかしそれにしても行列積の検算どうしましょう。とりあえず行列がお得意らしいR言語にお願い。検算してよかったデス。。。
※『RustにいればRustに従え』関係記事 index はこちら
※動作確認は、Windows11のWSL2上にインストールしたUbuntu20.04LTS上のrustc 1.64.0 (a55dd71d5 2022-09-19) で行っています。
行列の掛け算、素朴なバージョン
以下、行列積の計算の最初のバージョンであります。const ARRAYSIZEで定義されるサイズの正方行列2個、 array_a、 array_b を定義し、これに0から255までの乱数を詰め込みます。そして array_aとarray_bの行列積を計算します。各要素は8ビット幅までの乱数なので、掛け算すると最大で16ビット幅、それをARRAYSIZEだけ足し込むことになります。i32型であればARRAYSIZEが数百くらいであればビット幅が溢れることなくお茶の子さいさいの筈だと。
また前回の実験で、スタック上にとれるi32配列の最大サイズは(デフォルトのままなら)1400×1400要素であったので、100×100サイズとか400×400サイズくらいのサイズの行列2個を掛け算して同サイズの行列に解を詰めるくらいならメモリ的にも問題なかでしょう、と勝手な目論見。
でもま、まずは計算が正しく行えることのテストなので控えめにARRAYSIZEは10と。
use rand::Rng;
const ARRAYSIZE: usize = 10;
fn make_random_array() -> [[i32; ARRAYSIZE]; ARRAYSIZE] {
let mut temp_array: [[i32; ARRAYSIZE]; ARRAYSIZE] = [[0; ARRAYSIZE]; ARRAYSIZE];
for i in 0..ARRAYSIZE {
for j in 0..ARRAYSIZE {
temp_array[i][j] = rand::thread_rng().gen_range(0..256);
}
}
return temp_array;
}
fn print_array(nam: &str, ary: [[i32; ARRAYSIZE]; ARRAYSIZE]) {
println!("{}", nam);
for i in 0..ARRAYSIZE {
for j in 0..ARRAYSIZE {
print!("{},",ary[i][j]);
}
println!();
}
println!();
}
fn main() {
println!("mult_array1");
let array_a: [[i32; ARRAYSIZE]; ARRAYSIZE] = make_random_array();
let array_b: [[i32; ARRAYSIZE]; ARRAYSIZE] = make_random_array();
let mut array_c: [[i32; ARRAYSIZE]; ARRAYSIZE] = [[0; ARRAYSIZE]; ARRAYSIZE];
for i in 0..ARRAYSIZE {
for j in 0..ARRAYSIZE {
array_c[i][j] = (0..ARRAYSIZE).fold(0, |acc, x| acc + array_a[i][x] * array_b[x][j]);
}
}
print_array("A", array_a);
print_array("B", array_b);
print_array("C", array_c);
}
素朴版、計算結果
計算結果が以下に。AとBが乱数を詰めた配列。Cがお答えっす。
しかし計算はあっているのか?
行列計算が得意らしいR言語に検算お願い
最近よく使っている言語処理系ではScilab様やMaxima様も行列計算お得意みたいですが、今回はR言語にお願いして、上記結果の検算してみました。上の出力をコピペしてちょい加工してCSVにファイルに落とせば、以下のような操作で行列a と 行列 b の行列積を求めることができます。
なんだ行列積って、%*%、たった3文字か。ちょっと寂しいものがあります。計算結果をView()してみたところが以下に。上記の演算結果と全数コンペアしてない(手抜きだ)けど、まあ、多分、一致しとりますがな、きっと。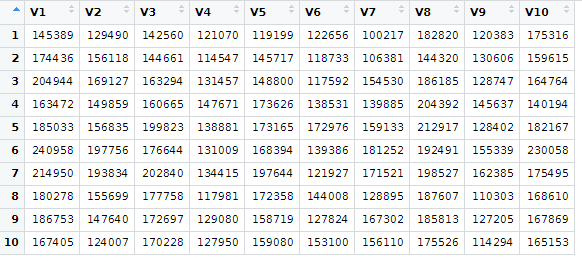
でも検算しておいてよかったです。実は初回はツマラナイやらかしで正しい計算できてなかったデス。修正できたのはR言語のお陰ね。次回はRustらしい機能でコードを書き換えたいと思います。