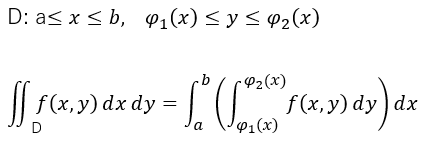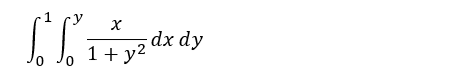前回の繰り返し積分は、積分範囲ｘ、ｙの上限、下限が定数で押さえられていました。つまりｘｙ平面でみれば積分範囲は長方形でした。今回は一歩前進？ｘに対してｙの範囲はｘの関数っす。積分範囲にマルでも三角でももってこい、という感じ。でもMaxima様にお願いしたら、何のこともなくお答えが求まると。何も考えねよ～
※「忘却の微分方程式」投稿順 index はこちら
※数学のお勉強のための以下の教科書（参考書、問題集？）の例題をMaximaの練習に使わせていただいております。
遥かなるかな太古の時代、大学生のときにこういう御本が欲しかったデス。
※以下のMaxima/wxMaximaバージョンで実習させていただいております。
-
- Maxima 5.46.0
- wxMaxima 22.04.0
例題１
例によって積分関数integrateにシングルクウォートつけて評価を一端抑制して式の形を愛でてから、ev(,nouns)で結果を求めてます。入力はこんな感じ。
Ex78_1: 'integrate('integrate(x/(1+y^2),x,0,y),y,0,1);
ev(Ex78_1, nouns);
例題の式は、読み易く清書するとこんな感じ。
でも上記の入力だと、意味は分かるけど、ちょっと汚いです。
でもお答えは求まりましたです。評価をお願いするだけ。ホント、何も考えてね～です。練習になりませぬなあ。
例題２
例題２は最初に小ネタ、assumeが必要です。assume忘れるといざ積分の段になってから、aはポジティブなの？それともネガティブ？などとMaxima様からご下問があります。メンドクサイので必要なところでは忘れずassumeと。
assume(a>0);
Ex78_2: 'integrate('integrate(x*y^2,y,0,sqrt(a^2-x^2)),x, 0, a);
ev(Ex78_2, nouns);
今回の「スンドメ入力」では、結構いい感じの積分の式が表示されたので特に清書はいたしませぬ。前回の冒頭に掲げた公式をそのまま適用している感じであります。
お答えを求めるのは、これまた一撃。いつもこんな感じで簡単に求まると良いな。練習にはならんが。