前回は先入れ先出しが可能なデータ構造 deque を使ってみました。今回は入れる順序には関係なく、入れたデータの大小関係によって取り出しの順番が変わる heapq を使ってみます。まさにヒープソートのアルゴリズムみたいです。端からデータをしまっていけば、取り出すときには大小関係順序通りに取り出せるので便利。ホントか?
※「MicroPython的午睡」投稿順 Indexはこちら
heapq
前回の collections.deque もそうでしたが、今回の heapq もフルPython処理系にも存在するモジュールのマイクロ版です。だいたいの仕様を似せてあるサブセット?中には不在のメソッドや機能もあるけれど、普通に使うところはほぼほぼそのまま使えるという感じです。MicroPythonの日本語版ドキュメントが以下に。
例によって、公式名称?は uheapq だけれども、MicroPython処理系内で呼び出すときは、頭の u を除いて heapq でOKっす。
実験用のソース
実験用のMicroPythonスクリプトが以下に。実験手順としては以下のような感じです。
-
- 中にタプルを要素として詰めているリスト hq をheapq化する
- この際、タプルの第1要素が大小関係を示すキーで、第2要素がデータと考えておく。
- heapq化されたhpに、第1要素に乱数、第2要素に順序数を載せたタプルを次々とheappushしていく
- タプルを詰め終わったら上から4個をheappopして内容を確かめる
初期状態は手動でタプルを詰めてあり、その後の乱数には手加減を加えてあるので、先頭2要素は確定ですが、後は乱数なので成り行きです。勿論、heapq中に詰めるのはタプルでなく、単なる数値でもよいです。
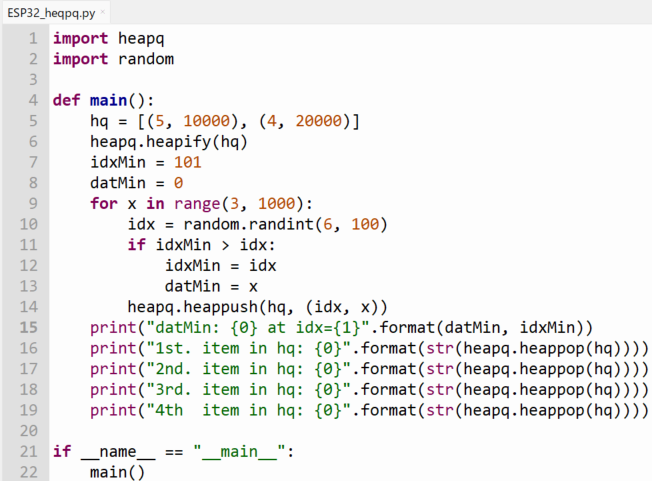
import heapq
import random
def main():
hq = [(5, 10000), (4, 20000)]
heapq.heapify(hq)
idxMin = 101
datMin = 0
for x in range(3, 1000):
idx = random.randint(6, 100)
if idxMin > idx:
idxMin = idx
datMin = x
heapq.heappush(hq, (idx, x))
print("datMin: {0} at idx={1}".format(datMin, idxMin))
print("1st. item in hq: {0}".format(str(heapq.heappop(hq))))
print("2nd. item in hq: {0}".format(str(heapq.heappop(hq))))
print("3rd. item in hq: {0}".format(str(heapq.heappop(hq))))
print("4th item in hq: {0}".format(str(heapq.heappop(hq))))
if __name__ == "__main__":
main()
実行結果
実機ESP32DevKitC上で実行しているMicroPython処理系で上記のスクリプトを実行したところが以下に。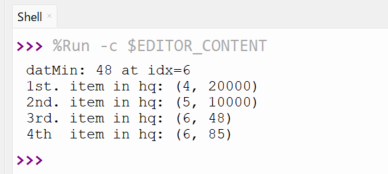
予定どおり、昇順で取り出せてるみたい。