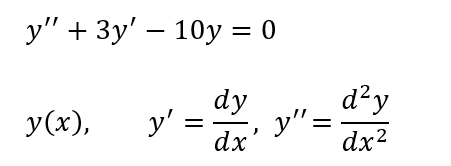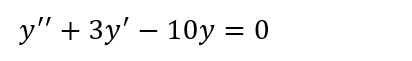約100回近い「単元」を乗り越えて今回から微分方程式に戻ることになりました。長かったです。とはいえまだ、Maxima様のオペレーションを固めるための反復練習の一環であります。最初はフツーの常微分方程式の一般解を求めるというアリガチなところから。しかし「一般解を求める」というところが意外にメンドイ?良い方法は無いのか?
※「忘却の微分方程式」投稿順 index はこちら
※今回からは数学のお勉強のための以下の教科書の例題をMaximaの練習に使わせていただいております。ただし御本家『培風館』様のホームページで検索してみるも掲載されていないようです。絶版? そのため以下のリンクは『Amazon』の通販ページであります。ご注意を。
※MaximaおよびそのGUIであるwxMaximaの以下バージョンを使用させていただいております。
-
- Maxima 5.46.0(x86_64-w64-mingw32)
- wxMaxima 22.04.0
常微分方程式の解法
遥かなる昔、以下の回で「常微分方程式の解法」に触れました。今回はその復習?であります。
忘却の微分方程式(32) 常微分方程式を解く その1、MathematicaとMaxima
まずは、数学の教科書の定石どおり、「一般解」を「解析的」に求める方法から練習したいと思います。上記の回で、その方針は以下のようにまとめられていました。忘却力の年寄は自分で書いて忘れていたけど。
-
- 微分方程式を定義する
- atvalue()関数で、初期値を定義する
- desolve()関数で解く
ここでポイントは1の方程式を定義するときに、「微分」の記述に ‘diff(~ などとスンドメ形(名詞形)で記述しておく、ということであります。そうしないとdiff()のところでMaxima様が微分を解こうと頑張ってしまいます。
今回の例題
数学の問題集的には、上記の表記だけでも「常識のある」よゐこは回答できる筈。しかし、上記の裏に以下の定義があることをアカラサマにしないとMaxima様にお願いできませぬ。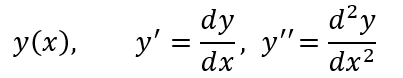
yはxの関数だったのね~。
解を求める
さてここで、上記の常微分方程式を解くための3ステップをおさらいすると、ステップ2のところで初期値(境界条件)を定義してます。特殊解じゃん。一般解にならないじゃん。。。どおする?
初期値自体をCとかテキトーな文字定数にしておけば、一般解になるじゃん
一応お答えは求まりました。しかし数学の「解答」的には黄色のマーカ部分こそテキトーな任意定数1個にまとめて「綺麗な一般解」にしておきたいデス。
ただし上記を一撃で任意定数に変換する技は持ち合わせておらず。まだまだじゃ。以下のようにして変形してみました。カッコ悪い。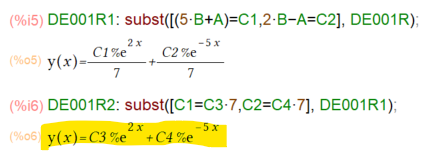
なんとか「一般解」風な形にもちこめました。後始末の方がメンドイ?