微分方程式のHelloWorld的例題の練習3回目です。前回は放射性物質の崩壊モデルでした。今回は単振動です。きわめて単純化。摩擦なしで無限に振動するアレです。ぶっちゃけ微分方程式を立てて解かなくても答えは分かっておる、のですが、やらずにはいられませぬ。Hello Worldだから。サガ?
※「忘却の微分方程式」投稿順 index はこちら
※数学のお勉強のための以下の教科書の例題をMaximaの練習に使わせていただいております。ただし御本家『培風館』様のホームページで検索してみるも掲載されていないようです。絶版? そのため以下のリンクは『Amazon』の通販ページであります。ご注意を。
※MaximaおよびそのGUIであるwxMaximaの以下バージョンを使用させていただいております。
-
- Maxima 5.46.0(x86_64-w64-mingw32)
- wxMaxima 22.04.0
今回の例題
後で角周波数ωでお答えを清書する予定です。
微分方程式を解く
微分方程式をMaxima様に渡せば、例によって1,2の3で答えがでます。こんな感じ。
atvalueで初期条件を渡したものの、assumeでk, mが正の値であると宣言しておかなかったです。お答えを求めるときに聞かれてしまいました。負のバネ定数、負の質量とかあると怖いですケド。
最後の結果の式がチト汚いのでω使って清書します。こんなんでどうよ。
本当はωtとしたいです。Maxima様にお願すれば、変数の順序の制御が出来たような気がしないでもない。でも調べるのがメンドイのでそのままね。
プロットせずにはいられない
お答えは求まったですが、前回、前々回とプロットしているので、今回だけプロット無とはいきませぬ。プロットといえば文字定数に何か数値を当てはめないとなりませぬ。初期位置X0に1,角周波数ωも1としてプロットする操作が以下に。
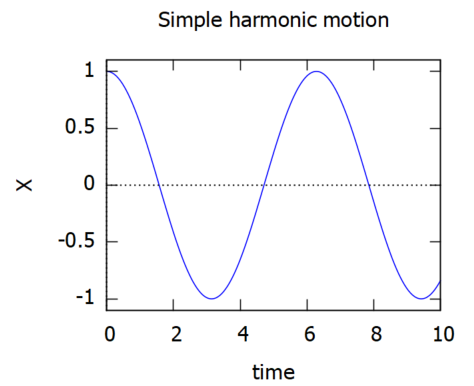
DE004P: subst([X0=1, ω=1], DE004W) plot2d(rhs(DE004P), [t, 0, 10], [title, "Simple harmonic motion"], [xlabel, "time"], [ylabel, "X"]);
見慣れたカーブよな。