
前回は、3階、4階の定数係数同次線形微分方程式でした。3階以上では伝家の宝刀、ode2が使えなくなるので、ちょいとメンドイdesolveにお願いしてました。今回は「非同次」です。教科書的にはもっとメンドそうな。しかし例題は2階デス。おっと ode2が使えるじゃん。教科書的なお教えをバイパス。いいのかそんなことで。
※「忘却の微分方程式」投稿順 index はこちら
※数学のお勉強のための以下の教科書の例題をMaximaの練習に使わせていただいております。ただし御本家『培風館』様のホームページで検索してみるも掲載されていないようです。絶版? そのため以下のリンクは『Amazon』の通販ページであります。ご注意を。
※MaximaおよびそのGUIであるwxMaximaの以下バージョンを使用させていただいております。
-
- Maxima 5.46.0(x86_64-w64-mingw32)
- wxMaxima 22.04.0
定数係数2階非同次線形方程式
教科書的には、こんな感じの「奴」です。
y” + ay’ + by = Q(x)
この解法としては、
-
- ともかく特殊解 η(x) を見つける
- 同次方程式 y” + ay’ + by = 0 の基本解を求める
- 以下のスローガンで非同次方程式の一般解が求まる「非同次方程式の一般解=同次方程式の一般解+非同次方程式の特殊解η(x)」
というステップをお教えいただいております。その際 Q(x)が以下であれば特殊解η(x)の形は分かっているのでラッキーっと(そういう言い方していいのか?)
-
- Q(x)がd次の多項式
- Q(x)が三角関数(A cos(αx) + B sin(αx))
- Q(x)が指数関数(A eβx)
しかし、2階です。ode2()関数の適用範囲内っす。伝家の宝刀 ode2()が使えるならば、いろいろメンドイ手順を踏まずとも、微分方程式を渡せば立ちどころに一般解が出るっと。
例題1
まずは、ode2()の御帰還を祝って1題。2階の非同次方程式ですが ode2()にお任せすれば「ほぼ」一撃です(今回は教科書的に整理された形にするのに最後にfactorかけてますが。)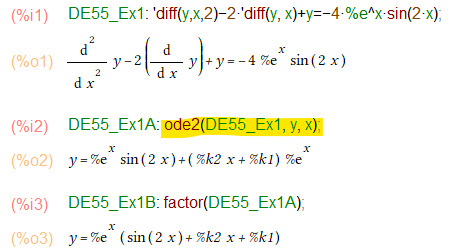
いい感じだな。
例題3、4、5
例題3、4、5と並べたのは、他でもありません。これら3題は微分方程式の左辺は共通です。こんな形。
y” – y’ – 2y =
そして右辺のQ(x)は、例題3、4、5の順に、上で列挙されておる多項式、三角関数、指数関数であります。教科書的には「未定係数法」を駆使して特殊解η(x)を求めることになるのですが、ode2()にお任せすると即一般解がもとまっちまいますぜ。
以下黄色のマーカ部がQ(x)、緑のマーカ部が特殊解η(x)部分デス。
やっぱり、ode2()の切れ味は良いなあ。お楽。