前回、地球の公転軌道を描いてみました。万有引力の法則、半端ないっす。でもね、ほぼほぼ円軌道の地球だけでは物足りませぬ。いかにもアリガチな長楕円軌道がみたいです。そこで彗星軌道(ハレー彗星に寄せているけど雰囲気だけ)を計算してみました。しかしスケーリングと誤差の問題発覚。手を抜くと誤差が酷いことになるのよ。
※「ブロックを積みながら」投稿順 index はこちら
※動作確認にはWindows 11の パソコン(64bit)上にインストールしたScilabの以下バージョンを使用しています。
Scilab 2024.0.0
今回は前回と同じフロー
今回は太陽と天体1個(いずれも質点)、その上、太陽は動かないことにしてしまった手抜きの前回のフローの再利用です。天体のパラメータのみ変更して異なる軌道を描いてます。フローの再掲が以下に。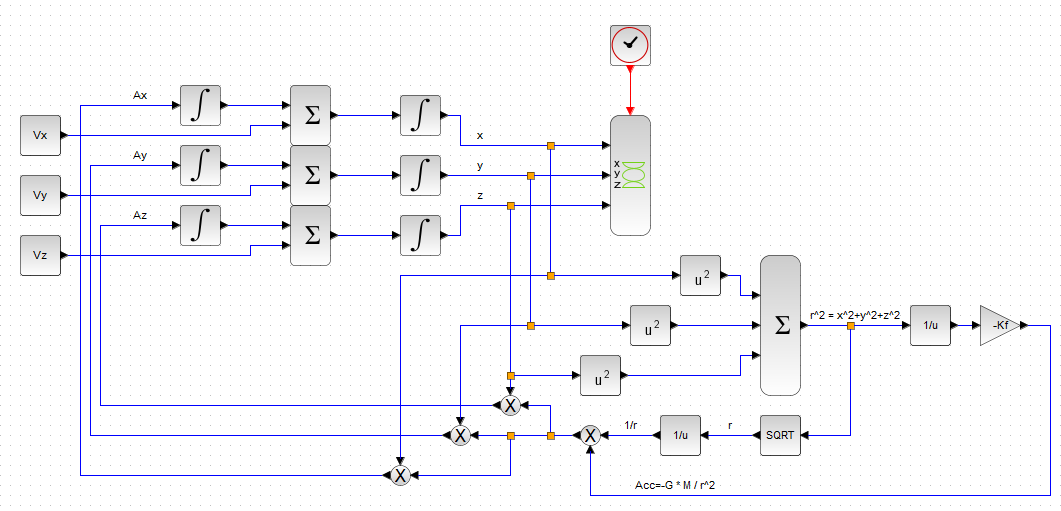
ニュートン大先生の万有引力の法則の威力をアカラサマにするものであります。
ハレー彗星に「寄せる」
彗星といったらなんといってもハレー彗星であります。周期的にやってくる彗星があることをハレー様が突き止めた大彗星であります。短周期彗星に分類されるみたいですが、短周期の中では「長め」です。
周期約75年
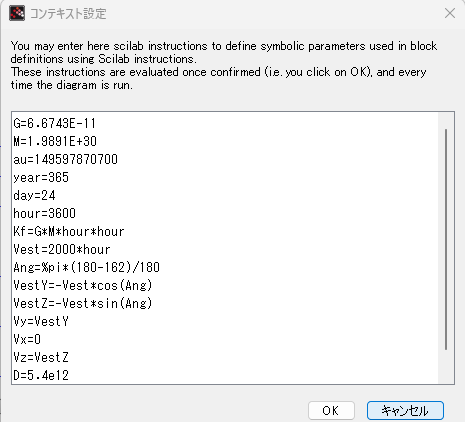
また、調べてみてようやく気付いたのですがハレー彗星、「逆行」してました。天の北極方向からみて反時計回りが順行。前回の地球は反時計まわりでした。しかし、ハレー彗星の軌道傾斜角が以下に。
軌道傾斜角 162.26°
180-162=18なので、赤道面とハレー彗星の軌道面のなす角は18°ということなのですが、ハレー彗星が他の多くのみなさんとは逆回りしているために、こういう角度で逆行を表現するみたいです。
近日点 0.58598au
遠日点35.08231au
今回のモデルでは、遠日点距離とそこでの速度が分かればシミュレーションできます。ハレー彗星の離心率などは調べられるので、かの「ケプラーの法則」使えば遠日点での速度も計算できるとは思ったのですがやってません。テキトーに「如何にも楕円」な軌道が描けるような速度を与えてます。手抜き。ハレー彗星に「寄せて」いるけど空想上の彗星、ということで。
シミュレーション上の問題
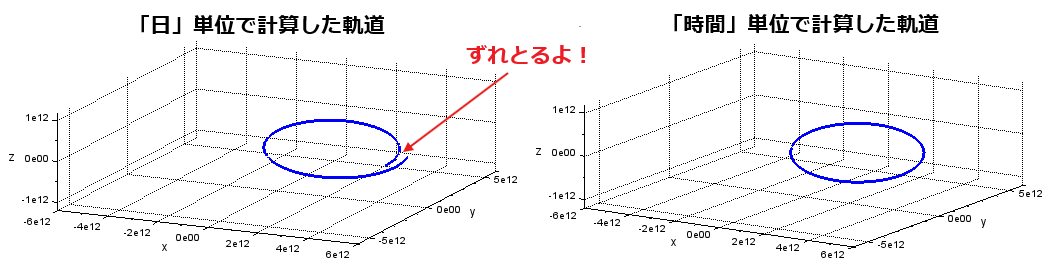
さて、ハレー彗星の公転周期が長めってことが、今回上記のモデルで問題を引き起こしました。前回は地球軌道を描くのに「秒」単位で計算したら計算がいっこうに進まん、ということで途中でキレて、計算単位を「時=3600秒」としてしまいました。結果、ビューンとした速度で軌道を描くことができました。今回、計算単位を上記のままにしたら、やっぱり計算が進みませぬ。今回も再度キレて、計算単位を「日=24*3600秒」に上げました。その結果が以下に。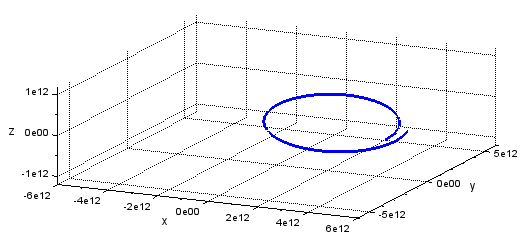
楕円が描けるハズが、遠日点付近がズレとります。考察するに、遠日点付近の速度は非常に遅いので日単位でズボラな計算しても大した誤差はでまいと思う反面、近日点付近は超高速で移動する上にカーブの曲がりもきついデス。そのため日単位の計算では大きく誤差が出るものと考えました。やっぱり変化が大きいものは手を抜いたらダメだ。
しかたないので、計算単位を「時」に戻して、計算が終わるまで放置プレイっす。その結果が以下に。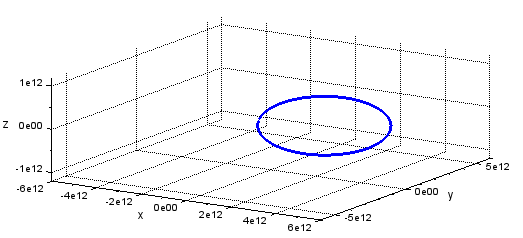
よかった、末尾がつながった。
なお、今回は結構デカイ軌道傾斜角なので、Z方向にも移動しているのが良く分かる方向からも眺めてみました。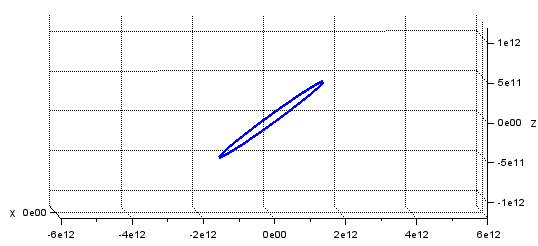
角度ついてるな~。
上記では遠日点速度はキリのよい2000m/sとしてますが、多分ホンモノのハレー彗星はもっとずっと遅いんでないかと。また、X方向積分の初期値として与えている遠日点距離はこれまたキリが良い35auとしてあります。
しょぼい図だけれども正確に計算するにはステップ細かくしないとダメみたい。トホホ。