懐かしのアナログコンピュータに触発されて、ついつい微分方程式の大平原に踏み込み、ScilabのXcosへとやってきました。ブロックダイアグラムを描いたらば、微分方程式が解ける優れものです。しかしね、そのブロックダイアグラムったら、微分方程式を書き出さねばとても描けない。抵抗１個にコンデンサ１個の回路でも、私の頭の中には思い描けない。回路図なら簡単なのに。
※「忘却の微分方程式」投稿順 index はこちら
RとCを直列に接続し、そこに電圧を印加する回路、今回はローパス・フィルタ風に、抵抗Rを介して容量Cに電荷をチャージする回路を考えます。さて、この過渡応答を得るには、これまでのところのXcosを使った「解法」であれば、その様子をまず微分方程式として書かねばなりますまい。ボケた頭で思い浮かぶのが、抵抗Rを流れる電流i(t)と容量Cに溜まる電荷q(t)を足したものが、印加している電圧V(t)に等しい、と。
左の式で良いのかしら。遥かな昔にそんな式を勉強した気もしますが、老人の記憶は危うい。しかし、まだ、このままではXcosで解けません。ちゃんとね「微分」方程式の体裁にしなければ。そういえば、i(t)のお陰で容量に溜まっていく電荷q(t)との関係はといえば、
qを時間で微分すればi
これもね、遠い昔の遥かな記憶ですな。ようやく微分が出てきた。１階の微分方程式になったので、これを整理して、書きなおします。いや～、式の変形も辛い。やりたくない、今はいろいろ良いものがある、数式処理に頼りたいくらい。なんとか封筒の裏側にボールペンで書きつけたのがこちら。
本当に、こんなもんで良いのでしょうか？錆びついた頭ではもうろうとして良く分からない。でもま、良いことにして先に進めます。
左辺はq(t)の微分、これを積分すればq(t)そのものが登場するので、まず、Xcosの真ん中に積分器を置いてその出力をq(t)とします、当然入力はq(t)の微分です。上の式からq(t)の微分というのは、電圧の時間関数V(t)に1/Rを乗じたものから、q(t)に1/RCを乗じたものを引いたものである、と。そのままそれをブロックダイアグラムにならべます。ただし、ここでは、簡単のため、R、Cみな1（抵抗1Ωはいいけれど、１Fなんて尋常でない容量だが、計算だけだしOKっと）、これで微分方程式部分は書けた。けれど、出力はCに掛かっている電圧にしないとな、やっぱり。するとｑ(t)をCで割ったらばよいであろう。それをグラフに描けばお答えが出る筈。それがこちら。
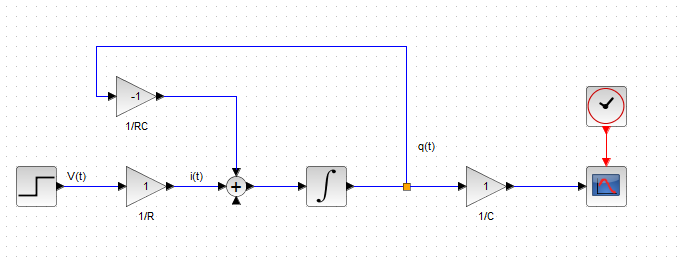ブロックダイアグラムは書けたけれども、直感的にRC回路なんだ、という雰囲気に乏しい。コメントを無くしたらもやはRC回路とは想像できない（まあ、それが数学の抽象化ということだよねえ。）
適当にシミュレーション期間など調整し、「電圧５Vのステップ関数」の「つもり」をV(t)として与えてみれば、御覧じろ。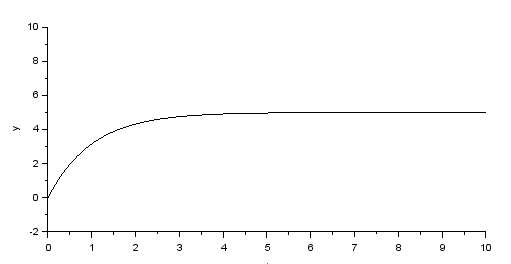
まあ、期待通りのエクスポーネンシャルなグラフ。微分方程式、間違っていないようです。しかしね、
LTspiceだったら、RとCと電圧源を置いて繋げば
一発じゃん。わざわざメンドクさい式の変形などせんでもよいです。大体、RC回路でこんな大変じゃあ、ちょっと回路複雑になったらもうどうしようもなくね。それにRとかCとか物理実体から遠ざかる方向だよね、デバイス的には「部品」が見えていて欲しい。
多分、想像するに、そういうことをお感じになった人も多いのではないかと。調べてみると、Scilab Xcosには、上のように「数学風」に微分方程式の形で問題を解くのでなく、
抵抗とか、コンデンサとか、要素を接続したら問題を解ける
部品共が存在しました。
Modelica
というお名前のついたブロック部品群です。どうもModelicaというのは、独立の物理モデリング用の言語であり、ライブラリであるようで、それがXcosにも取り込まれて使えるようになっているらしいです。当然Xcos以外の処理系でも使用可能とのこと。この後、いろいろ使ってみながら調べてみる予定でいます。
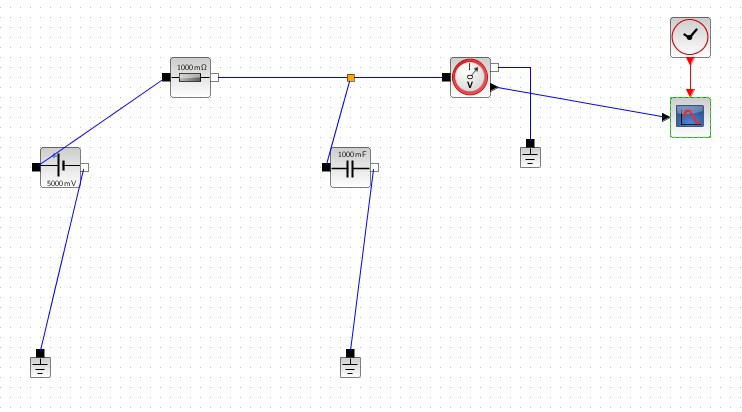
さすれば、Xcos上でModelicaのブロックから、抵抗器、容量、電圧源を取ってきてつなげてみます。これならLTspiceと変わらない（今はSpiceも図で書けるよな、昔はFortran式のテキスト入力だったもんね。今でも裏ではソースが出来ているけれど。閑話休題。）
しかし、Xcosの上のModelicaなかなか扱いずらい。部品をローテイトしながらRCのローパスフィルタ風にいい感じに並べた後、各要素のパラメータを書き込んでみたら、ローテートした回転が戻ってしまった。図がぐちゃぐちゃだあ。
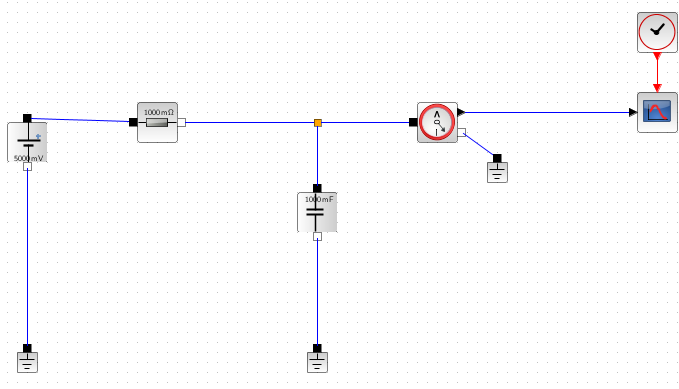
なお、Xcosのグラフ表示ブロックは、黒三角のポートで、Modelicaのブロック類は四角のブロックなのでした。ここに深くて暗い河がある、と。それを渡るために、電圧センサなどというブロックがあり、そいつが四角と三角の橋渡しをしてくれるのでした。これを実行すれば、こんな感じ。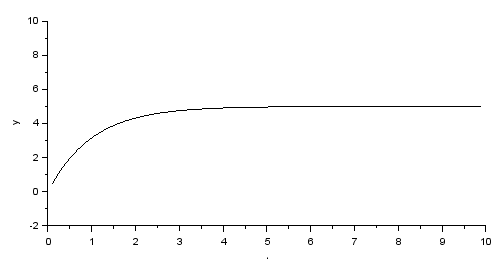
上の方の別なグラフと同じ波形（回路同じなのだから当然）ですが、ちゃんと別にキャプチャしましたよ。ちゃんとModelicaモデルでも動作はするね。
しかし、Modelicaの場合、Xcosの裏側にいるScilabの画面を見てみると大層な出力がでてきます。こんな感じ。
Xcosの普通のブロックらは、Xcosの中にそのまま動く実体があるようですが、Modelicaの方は、Cのプログラムとして裏側でコンパイルされ、実行されておると。何回か前に、私のScilab環境、コンパイラ使えるかな、とチェックしておりましたが、それがここで生きました。
それにしてもModelicaのブロックダイアグラム、醜いので、もういちど要素をローテイトしなおし、多少場所を変更してみました。まだ醜いけれど、まあ、いいか。結線する前にパラメータセットしないとダメ、というのは私の使い方になにか問題があるのか、バグなのか？これも調べてみないと。
Modelica調べてみると、電気回路に使うより、もっといろいろ他分野で活躍するようなものらしいです。まあね、電子回路ならSpiceあるからね。
Modelica調べ始めると、段々、微分方程式そのものから遠ざかりそうですが、面白そうなのでも少し。