
初回、前回と2回続けて、コロナなどの伝染病の流行モデルの中で一番簡単そうなSIRモデルの微分方程式を、Scilab/Xcosのブロックダイアグラムで「解いて」みました。そして、前回は3つも存在するゲインブロックの「もやもや」を解消しました。今回は積分ブロックの「もやもや」に決着つけたいと思います。なかなかSIRモデルから抜け出せませぬ。
※「忘却の微分方程式」投稿順 index はこちら
さて、前回は、信号を定数倍する「ゲイン」ブロックが、3つもあるのだけれど、そちらが機能的には皆等価であり、なにやら歴史的な経緯なのか、何なのか、そのうちの2つは今後の使用は非推奨ということでありました。
今回、気になっているのは、初回、前回と積分のために使った
INTEGRAL_m、まさに積分記号で積分にきっと間違いなし
と、
INTEGRAL_f、ラプラス演算子sで割るのは積分だったっけ?
という2つのブロックであります。以下のXcosのパレットブラウザを御覧ください。
だいたい、_fと_m、どういう使い分けをしているのでしょう。(実はFortranで実装されているのが_fなどと勝手仮説をたてたのですが、反例相次ぎ破綻。どこかに書いていないのか?)
こうしてみると、ブロックの見た目は全く異なります。1/sなどと書かれると、ラプラス変換でしょ、伝達関数用?みたいな印象を受けるのですが、
どちらも普通に時間に関する関数を積分できる
ブロックであります。本当にラプラス演算子 s を使って伝達関数で記述できるブロックは、1行上にある
CLR
というブロックの方です。分子が1、分母が1+sになっているので上のような見た目になっている。
さて、積分に戻ります。実は気になったのが、Xcosの利用例をいろいろ眺めていて、「1/s」 の方で描かれているものと「積分記号」の方で描かれているものの両方があり、混在させているような例は見当たらなかった、ということがあります。まさに
1/s「流派」 と 積分記号「流波」
私は、図らずも積分記号で始めてしまいました。後で離散的なモデルを扱う場合には、sに対してzが登場します。2つのモデルの対比など考えるとsで書く方が良いような気もする。でも、実際に時間に対する関数を積分しているという点では、積分記号の方が直感的でおおいに分かり易い気もする。。。
論より証拠、前回のSIRモデルの積分ブロックの1個を1/sで書き換えてみました。流派逸脱、見苦しいこと間違いない。
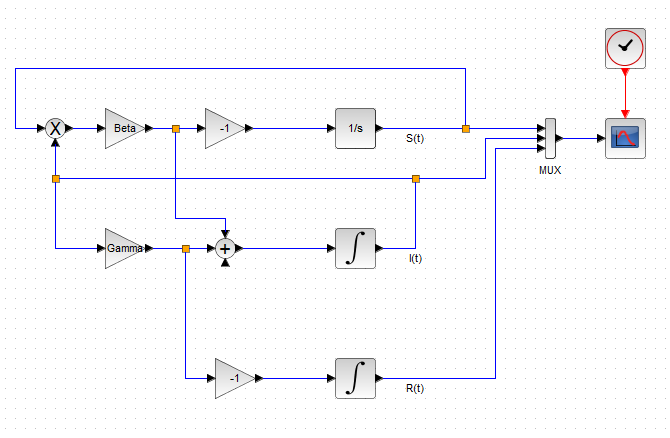 しかし、上のお見苦しいブロックダイアグラムでも、これを実行すれば、前回とまったく同じ結果が得られます(グラフは省略)。なお、積分初期値を前回と同じ値にしておくことを忘れずに。これを忘れると、とてもつまらないグラフになります。人口0人、誰にも感染する訳はない。
しかし、上のお見苦しいブロックダイアグラムでも、これを実行すれば、前回とまったく同じ結果が得られます(グラフは省略)。なお、積分初期値を前回と同じ値にしておくことを忘れずに。これを忘れると、とてもつまらないグラフになります。人口0人、誰にも感染する訳はない。
さてしかし、実際に2つを並べてみると、その違いも明らかです。1/sのブロックの方のパラメータは以下のように初期値のみ。
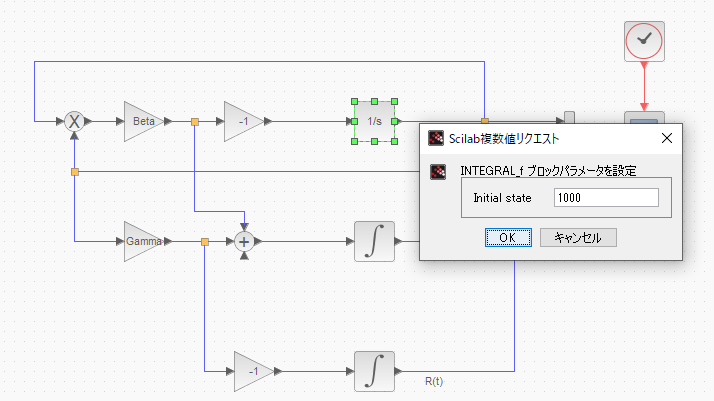 これに対するに、積分記号の方のブロックには、初期値以外のパラメータも多数。明らかに実装が異なります。
これに対するに、積分記号の方のブロックには、初期値以外のパラメータも多数。明らかに実装が異なります。
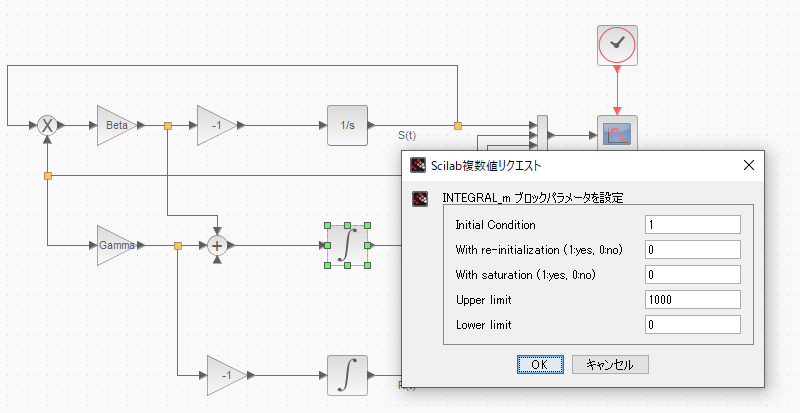 調べてみると、1/sの方の実装はFortran、積分記号の方はCでした。なお、前回も参照した、
調べてみると、1/sの方の実装はFortran、積分記号の方はCでした。なお、前回も参照した、
を再び参照してみると、
- 昔、INTEGRALという名のブロックがあったが、現在ではパレットから除去されている。(今のINTEGRAL_mと同等。なぜ削除されたのかは不明。)
- よりシンプルな積分がINTEGRAL_f(1/s)として実装された。
- 1の積分記号の見た目と機能は、多機能なINTEGRAL_mという名で継承された。
ということのように想像されます(間違っていたらごめんなさい。)
まあ、結論は、シンプルな積分するだけなら、どちらでも良い(でも実装がシンプルな分、1/sの方が速いのかも??)、上限サチらせたりとか、より高機能な実装が欲しい場合は、積分記号の方を選択、という感じでしょうかね。
Xcos、なにげに奥が(闇が)深いな。次回あたり、別な微分方程式に進みたいのだけれど。