一昨日、ラズパイ3のソフトウエアをupdateしていて気づいたのがWolframです。600MBくらいのダウンロードサイズ「でか」、ということで気づきました。そう言えば無料で使えるとあって、嬉しくインストールさせていただいたのですが、完全に忘却の彼方にありました。折角なので使い方勉強しよう、そして忘却の微分方程式に使おう、と。
※「忘却の微分方程式」投稿順 index はこちら
相当前にRaspberry Pi 3をセットアップしたときに、「無料で使える」ということでインストールしてしまいましたWolframとMathmaticaです。遥かな昔、買ったらお高いソフトウエアとして記憶に残っていて「憧れていた」ためです。太っ腹？なことにRaspberry Pi 上では無料で使えると。しかし、インストールしたのは良いのですが、そのまま使わずディスクの肥やしになとりました。こりゃモッタイない。
Raspberry Pi上で無料で使えるWolfram、Mathmatica
しかしね、Raspberry Pi 3のセットアップのときにインストールした記憶はあるのですが、Raspberry Pi 4の時にはまったく記憶にありません。なぜ？ 調べてみると理由は直ぐにわかりました。このRaspberry Pi専用バージョン、NOOBSにバンドル（別途インストールも可能らしいですが）されていたのです。Raspberry Pi 3にRaspbian OS(当時はそう呼ばれていた）インストールしたときはNOOBSを利用しました。しかし、Raspberry Pi 4にRaspberry Pi OSをインストールしたときはRaspberry Pi Imagerを利用でした。OSのインストールの方法が異なったために、Pi 4の時にはインストールしてませんでした。
実行速度は遅いけれどもインストール済のPi 3のまま練習予定。無料だし。
なお、Raspberry Piで無料でWolframさせてくれる件については以下のページに説明があります。
Raspberry Piを利用したWolfram言語プロジェクト
上記のページ内から、チュートリアル的なものとして以下へのリンクがあります（もち英文。）
Getting Started With Mathematica
しかしね、以下には、立派な日本語のチュートリアルがありました。ちゃっかりこちらを読みながら練習させていただくことにいたしました（ぜんぜん数学を学ぶ学生じゃないんだけれど、すみません。）
MathematicaとWolfram言語 数学を学ぶ学生のための入門チュートリアル
しかし、このチュートリアルをそのままやるだけでは芸が無さすぎです。Mathematica欲しいなあなどと分不相応な欲望を持ちつつ、私のような素人にはなくてもいいかと思えてきたのは、他にもある、いろいろなソフトウエアのお陰であります。その中でも
Maxima（もちろんフリー）
は、数式処理ができるということで、かなり「ガチ」で競合する？（といいつつ、Mathematicaとは異なる部分も多いですが）のではないかと思います。Maximaにしても時々思い出したように使わせていただく程度なので、身についちゃおりませぬ。でもま、ラズパイ３上でMathematicaのチュートリアルをやり、同様なことをPC上のMaximaでもやる、と。同じことを２回やれば多少は憶えるんでないかい。。。比べてみれば、お互いの強み弱みもわかるやいなや。
Raspberry Pi OSのGUIメニュー
さて、手元のPi 3のGUIのメニューを開くとこんな感じです。プログラミングの部に Mathematica と Wolfram が存在します。
今まで開いたことが無かったので知らなかったのですが、上記の場合 Mathmatica がGUIを持つアプリケーションで、Wolframは「素」の言語処理系？という感じです。実際 Wolframを起動するとこんな感じ。
上記を見ると分かるとおり、Wolfram言語というのはMathmaticaカーネル？であるみたいだし、MathmaticaのGUIに配置するCELLにWolfram言語のCELLがあるわで、どうも２つは一体にして不可分の関係なようです（勝手なこと書いて大丈夫か、よく知らないのに。）
入力
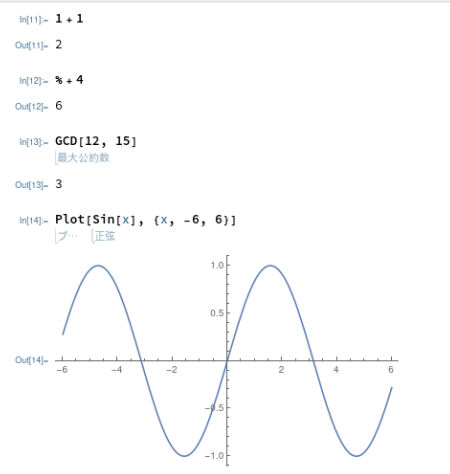
さっそく上記の日本語チュートリアルから最初の項目「入力」を実習してみます。最初は Mathematica から。
日本語設定しているので、こまめに日本語のガイドなど出るなと流石なUIの良さがヒシヒシと感じられます。また、Mathematicaにあって Maxima にない強力な機能が、
自由形式
みたいです。「自然言語」（といっても英語）で書いた文章をMathematicaの式にしてくれる機能。入力セルの冒頭で “=” を打つと発動します。でもね英作文が辛い人にとっては宝の持ち腐れか。トホホ。。。
一方、Maximaと共通するのが、式を評価するときには SHIFT+Return（単なるReturnは「改行」の意味）、前回の結果を参照するときは “%” といったお作法でしょうか。
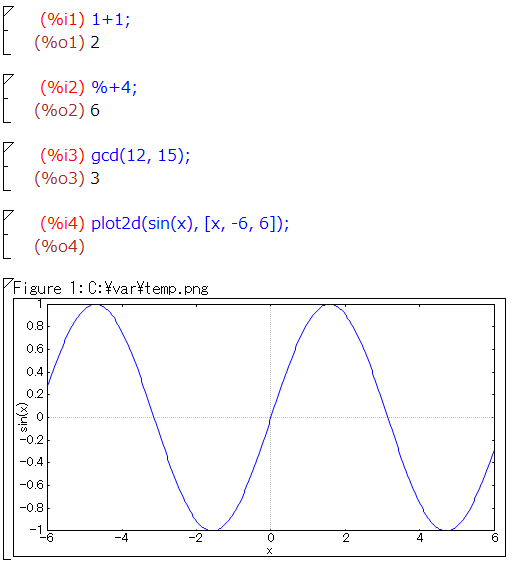
上記とほぼほぼ同じことを Maxima でやってみたのが以下です。
Mathematicaとの違いと言えば、以下です。
- 最小公倍数を求める関数は gcd と小文字。また関数の引数は()で囲む
- ２次元プロット関数は plot2d だが、これは外部プログラムである定番のグラフ描画ソフトウエア gnuplot を呼び出している
- リストは [ ] で囲む(Mathematicaは { } )
外部プログラムのプロット関数を呼び出しているためか、plot2d関数を呼び出すと別ウインドウでグラフが開きます。そのウインドウ上でプロットサイズなどを調整の上、ファイルとして書きだした後、画像としてグラフを取り込む方式のようです。一発で同じノートブックの中にグラフが現れるMathematicaと比べるとひと手間かな。
※2021/10/03追記: wxMaximaでwxplot2d関数を使うと別ウインドウは開かず、即座にノートブックの中に取り込まれて表示されます。
「リスト」の扱い
続いて、先ほどちらっと出てきたリストの扱いです。まずはMathematica。
上記のようにリストにスカラ値を演算すると、リストの各要素に作用します。リストの特定要素を取り出すときは [[ ]]で要素番号を囲みます。番号は数学系のソフトではお馴染みの１始まり。連続した数列を生成する場合は Range[]関数。
これに対するMaximaがこちら。
先ほど述べたとおり、Maximaでのリストは角カッコです。要素番号の指定も同じ角カッコ。リストとスカラの混合演算のやり方や要素番号はMathematicaと同じみたい。連続した数列を作り出す関数は makelist() 。引数が多いですが、第１引数に各要素値を生成する式、第２引数にインデックス、第３引数に下限、第４引数に上限を与えて生成です。
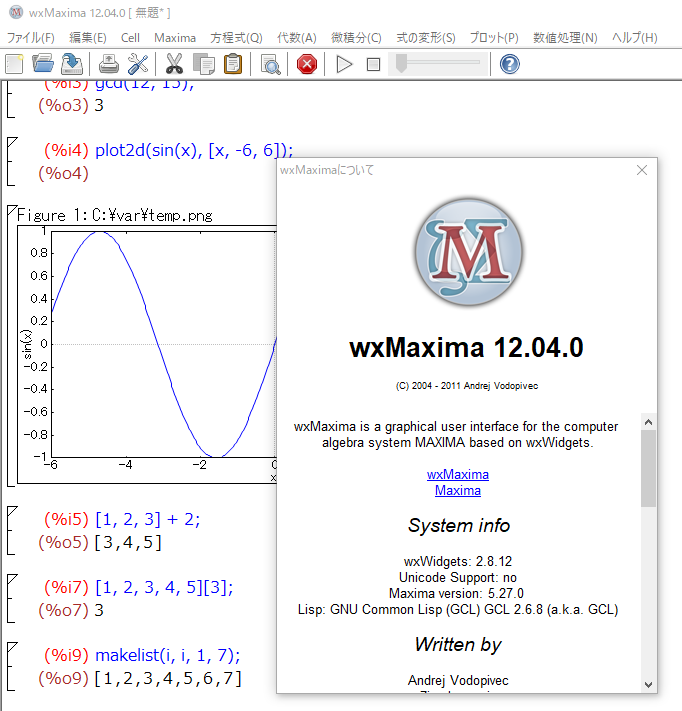
最後になりますが、本稿で使用させていただいたMaximaのバージョンは以下です。GUIであるwxMaximaは12.04.0ですが、Maxima本体は 5.27.0です。ちょっと古いかもしれない。
忘却しないように、チャキチャキ実習しないと。