今回は、Wolfram-Mathematicaのお手軽さというか取っ付きの良さにMaximaは完敗という感じです。まあ私がMaxima知らないのがダメなんだけれど。同じことは多分できるのだけれどもそこまでの道のりが遠かったです。テーマは「幾何」。幾何っていっても図を描いたりなんだけれども、なんだかな～
※「忘却の微分方程式」投稿順 index はこちら
学生でもないのに以下のWolfram社のドキュメントで学ばさせていただいとります。
MathematicaとMaximaを同時に使えるようになろうという野望にもとづき、MathematicaでやったことをMaximaでもやりという感じ。ちなみにMathmaticaはRaspberry Pi 3上の無料バージョンです。すみません（胸に手を当てて考えると、スマホ版のWolfram Alphaは、相当昔に「購入」した気がします。）
円盤を描く
Mathematicaで円盤（Disk)を描いてみます。いつもながら明快なお名前の関数を呼べば、適当に描いてくれます（何も指定しないと原点中心に半径１のDISKになるようです。）日本語でガイドも出てくるので迷うこともありませぬ。
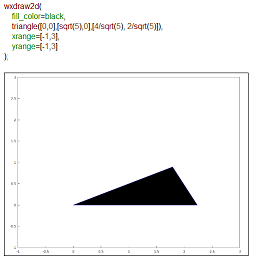
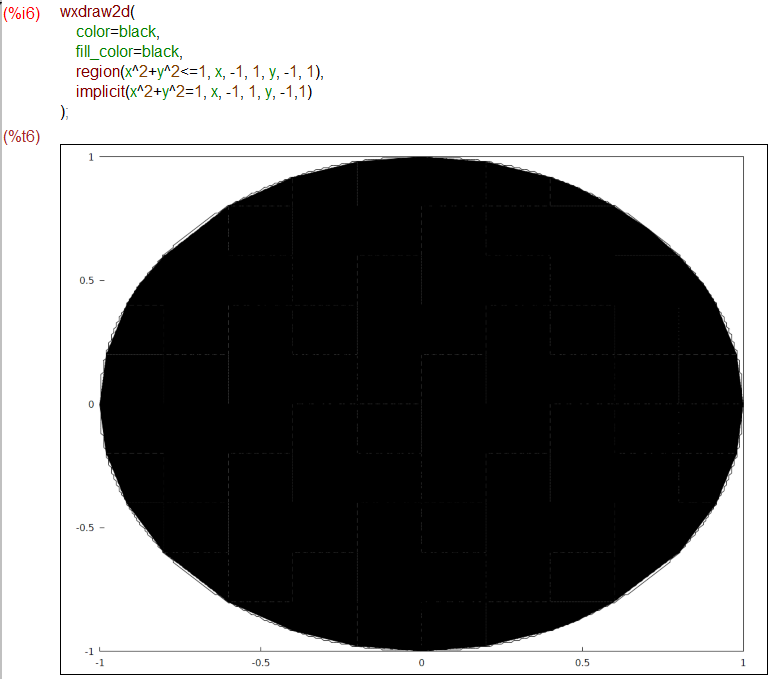
上のMathematicaと同じことをMaximaでさせるべく、最初にやってみたのが以下です。円の不等式の内部を塗りつぶさせるという前回取得の技。
しかしね、Mathematicaのシンプルさ、明快さにくらべると大分メンドイ。そこでMaximaのマニュアルを調べてみると、Graphics Objectsというものがあるじゃありませんか。日本語のマニュアルは以下に
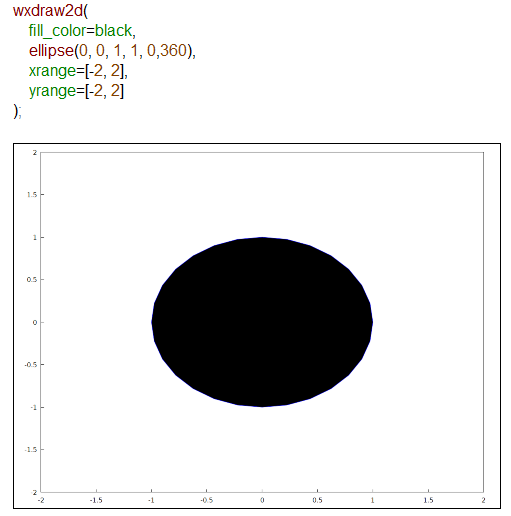
Graphics Object使ってみたものが以下です。上の「技」よりははるかに明快。何といっても式が出てこないもの。でもな～縦横比などどうやって調整したら良いのだろう？Mathematicaの方はRaspberry Pi 3にVNCでPCからリモートで接続しているのだけれど画面キャプチャすれば、ほぼほぼ正円に見えます。こういうところに違いがあるなあ。
長方形（レクタングル）を描く
流石にMathematicaも対角の座標くらいは必要。
Graphics Object使えば、Maximaもそれほど変わらない。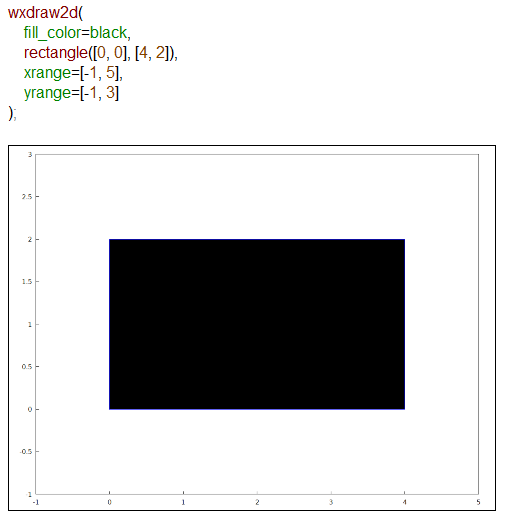
円盤と長方形の組み合わせ
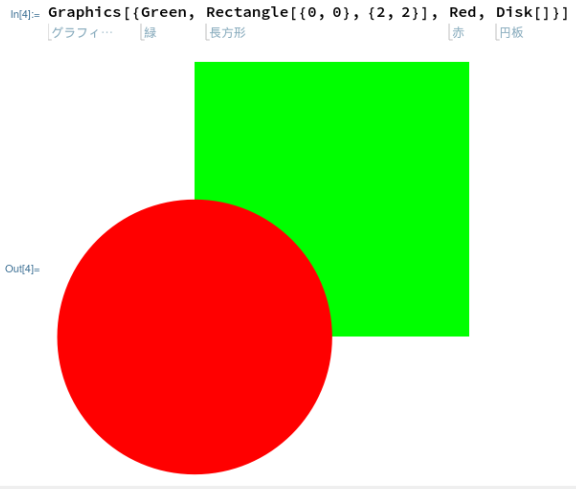
Mathematicaスタイルは、色と図形オブジェクトをリストにして渡す感じなのね。
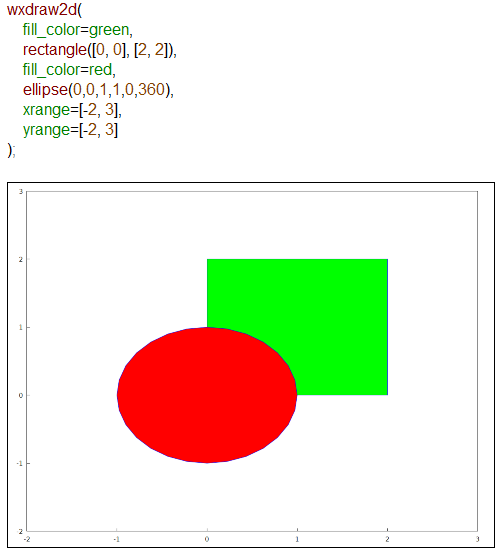
Maximaの場合は、Graphics Objectを背景側から順番に描いて行けばよろしかろうと。こんな感じ。
三角はMathematicaだな
Mathmaticaであると、「三角形」という実在を定義する関数あり、中身を見れば頂点の座標です。それをArea関数に渡せば面積が得られ、Graphics関数に渡せば図形が描かれる、と。直観的な操作ができる「出来合いの関数」があってとてもらくちん。
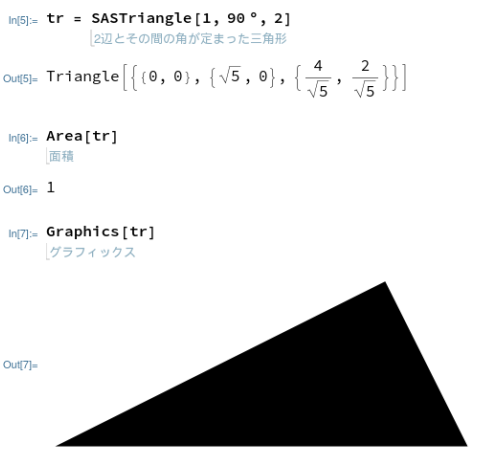Maximaで同じような関数無いか、探してみたんですが見つかりませんでした。３角形の頂点の座標やら、面積やら、多分中学生の数学で求まる「筈」なので、Maxima使えば計算はできる、そういう関数を定義すれば良い、とは思ったものの、元気ないです。一瞬で断念。
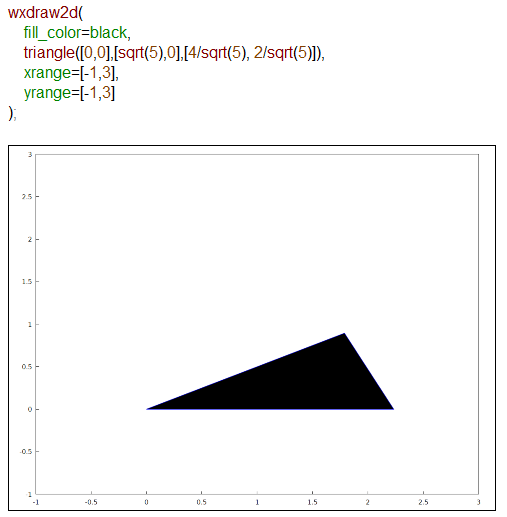
まあ、Mathematicaで頂点座標が出ているのでせめて図だけでも描こうということで描いたのが以下です。
次は３次元だ
Mathematicaは、２次元でお手軽にやったことを３次元でもやるのです。球を描く、そして体積を計算するなどお茶の子さいさい。
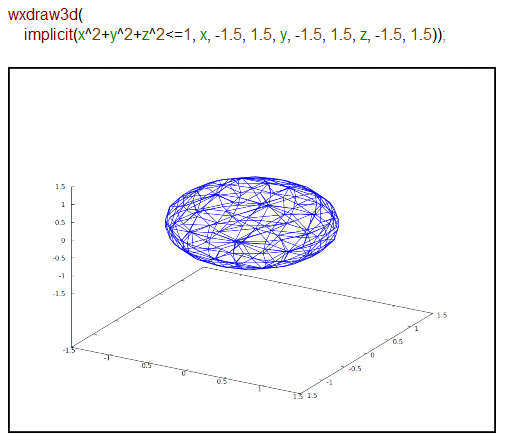
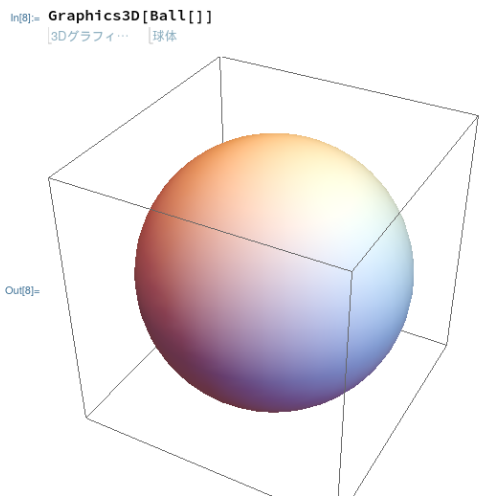勿論、Maximaでも「計算はできる」はずではあるのですが、元気がいります。無理。ここでも球らしきものを描いてお茶を濁します。しかし、縦方向がつぶれた感じの比率になるの、調整したいな～。どうすんだろう。
なお、Maximaでも3Dオブジェクトが存在し、以下の
spherical
という3Dオブジェクトを使えば、球も描けると「分かった」のですが、パラメータが多いんだ。アジマスとか。。。考えているうちに夜が明けてしまう（眠くなるの間違え。）