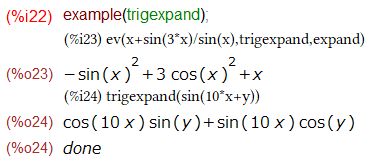今回は三角関数なんですけどね、正直１回じゃ理解するの無理。特にMaximaは使える関数とオプション制御の変数を適切に組み合わせないと所望の結果にたどりつけませぬ。今回は、とりあえずMathematicaのお題をなぞって、次回また演習してみるしかない。大丈夫か？
※「忘却の微分方程式」投稿順 index はこちら
今回のお勉強の題材は、Wolfram社の以下のドキュメントです（いつもながら学生でもないのに使わせていただいてます。）
Mathematicaのチュートリアルなので、Raspberry Pi 3上のMathematicaであれば、そのまま打ち込めば動きます。それにMathematicaはいろいろ気を回してくれるし、日本語のガイドまで出るしで優しい。しかし、例によってMaximaはツンツンしてます。知らないと手も足も出ない感じ。
早速、最初の課題から。Mathematicaに「SinをCosで割ったらTanかね」、と問いかければ、Trueとお答えが返ってきました。例によってSinなどの関数名が大文字で始まること、関数の引数を大かっこで囲うこと、等しいは＝＝（イコール・キーを２回押す）といったMathematicaのクセに慣れておれば簡単です。
一方、Maximaはと言うと、等しいは = （イコール一つ）で記述でき、関数名は小文字始まり、引数は小カッコ囲い、と慣れた感じの見た目なのです。しかし、ただ式を書いただけでは、真とも偽とも答えてくれませぬ。以下の例題の下の方、%i4（４番目の入力）とその答え%o4にあるように、美麗に式を書きなおしてくれる(GUIのwxMaximaの場合）だけです。真偽を評価させるためには if文を使うなど真偽を評価せざるを得ないようにしないとなりません。そこで 式の後に “and true” などと書けば、andは論理積なので真偽を評価せざるを得なくなります。
しかし、ただsin割るcosはtanみたいな記述(%i1)では false というお答えになってしまいました。一方(%i2)のように関数trigreduceにsin/cosの式を渡してやれば、その式を変形し、その結果として true を返してきます。ツンデレか？
さてお次は、アークタンジェントの値を求めますです。Mathematicaは大文字で書き始めるArcTan関数です。
こちらはMaximaも似たようなもんです。ただし関数名は atan と、プログラマにはおなじみな雰囲気のお名前。
確か、atanには、プログラマには伝統的にお馴染みの２引数をとるスタイルの関数もあったかと。
お次は三角関数のときによく使う定数の入力。Mathematicaは、数式の入力時から見た目の美しさにこだわっているみたいで、πとか、°（度）とかもESC押してpiとかdeg押してESCまた押しみたいなシーケンスで入力可能です（べき乗のCTRL＋６と同じで、美しい見た目だけれど手数が増えてメンドイです。Mathematicaでも普通にPiって書いても大丈夫みたいですけど。）
一方、wxMaximaは、出力時にはGUIに綺麗に式を「描いて」くれますが、入力時点では裏の本体Maximaにそのまま文字列を渡すのだと思うので、入力はアスキーキャラクタのままです。また、ラジアンでなく度で表記するのは見つかりませんでした。自分で変換しろよという感じ？とりあえず文字色は変えて見やすくしてはくれます。
次は、三角関数の式をいろいろ変形。まずはMathematica側の例題から。
Maximaにも trigexpandはあり、動かしてみるとMathematicaの同名（ただし大文字はじまり）の関数と同じお答えを戻してきました。しかし、３角関数の因子分解はどうしたもんだろう？使えそうな関数に端から食わせていましたが、皆挙動が違います。当然だけれども。関数の違い以外にもその挙動を制御するための変数があるみたいです。どういうときにどれを使うのか知りたいです。次回はこれだな。倍角公式とか半角公式とか、高校の数学の演習をやってみるしかない。
MathematicaのSolveは、結構柔軟（ゲテモノ食い？）で、なんでも食って解を与えてくれるみたい。便利。定義域の指定も簡単だし。
一方、Maximaのsolveは、ちとメンドそう。これまた後で調べないと、とても言うことを聞いてくれなそう。
とりあえず舐めてみて、ショッパイのは分かったので、味わう？のはまた今度だな。ちんたらしてるな、自分。