前回、浮動小数点の加減算をやりました。その前に例外を「味わう」ために浮動小数点の除算をやっています。そこで今回は必然の乗算です。ただ掛け算が出来たと喜んでも芸がありませぬ。RISC-Vには、普通の掛け算命令だけでなく、積和演算命令もあります。信号処理(積分)などするときはこちらの方が「普通」。今回はこの2つを比べてみる、と。
※「ぐだぐだ低レベルプログラミング」投稿順indexはこちら
※2022年2月16日追記:しょうもないバグ見つけてしまいました。文中のソースと結果について、お詫びして訂正させていただきます。
積和演算「掛けて、足して、しまう」は良いコンパイラなら使うべきときに使ってくれる命令です。積和算は「ちょっとした」信号処理から大規模なシミュレーションまで活躍していると思います。単純な掛け算命令と足し算命令を2つ続けてやるのとは違いがあるからです。積和命令のメリットをまとめると以下のようになるかと思います
-
- 2命令が1命令で済むので命令のフェッチとデコードの負荷が減る
- 乗算器と加算器を内部で接続して演算するので実行サイクル数が短い
- 丸めを最後の1回で済ませるので微妙に精度が違う
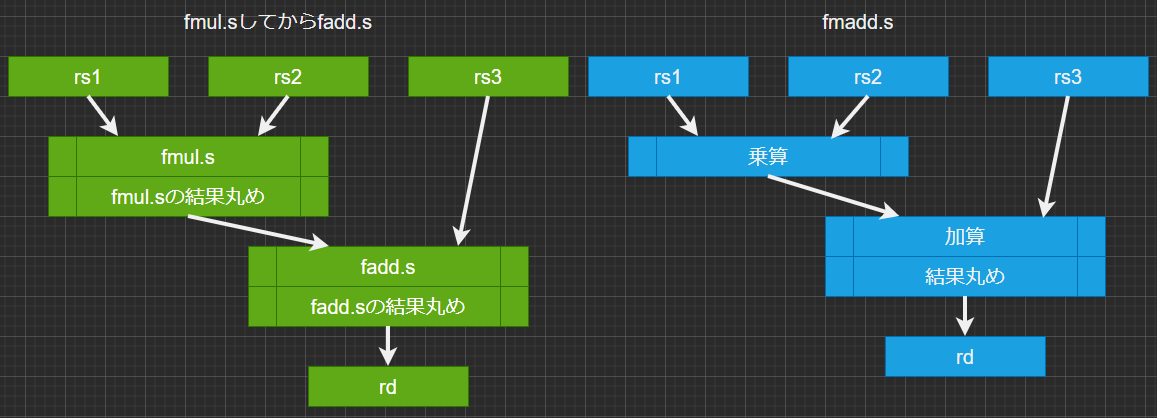
特に3の項目については冒頭のアイキャッチ画像に掲げました説明図をご覧ください。単独の乗算命令と加算命令を組み合わせるとそれぞれの命令の末尾で「丸め」が入ってしまうのに対して、積和命令では乗算器を通った直後には丸めが入りません。精度的には有利と思います。
浮動小数点演算命令をお使いになる、お兄さん、お姉さん方は速度にも精度にも厳しい人ばかりだと想像するので、この辺の細かい違いには敏感ではないかと思います。
実験用の「積和」関数
以下にRISC-Vの単精度浮動小数点演算命令のテスト用のソースコードを示しました。64bit RISC-V搭載、Kendryte K210で実機テストをしておるものです。
2つ関数を並べましたが、どちらも3個の単精度浮動小数点数、arg1, arg2, arg3の間で
result = arg3 + arg1 * arg2
という計算をするのです。しかし、以下の点が異なります。
-
- tst_Fmult_fadd()関数 単純乗算 fmul.s 命令と単純加算 fadd.s 命令利用
- tst_fmadd()関数 積和演算 fmadd.s 命令利用
両者の速度の差を見るため、rdcycle命令でサイクル数を調べています。既に経験したとおり、浮動小数点演算命令のように長い演算パイプラインを通る命令のサイクル数の計測は一筋縄ではいかないものです。今回は、2つの関数の中のテストシーケンスのサイクル差から、単純命令の組み合わせと積和演算命令のサイクル差を求めてみようと思います。似せたシーケンスのサイクル差であれば、かなり確からしいのではないかと、勝手な目論見であります。
テスト用の関数のソースは以下のとおり。
void tst_Fmult_fadd(uint32_t tnum, float arg1, float arg2, float arg3)
{
uint32_t nCyc = 0;
TestFloat f0S, f1S, f2S, f3S;
f0S.fDat = 0.0;
f1S.fDat = arg1;
f2S.fDat = arg2;
f3S.fDat = arg3;
asm volatile("fmv.w.x f0, %[Rd]\n\t"
"fmv.w.x f1, %[Rs1]\n\t"
"fmv.w.x f2, %[Rs2]\n\t"
"fmv.w.x f3, %[Rs3]\n\t"
"rdcycle t0\n\t"
"fmul.s f0, f1, f2\n\t"
"fadd.s f0, f0, f3\n\t"
"fmv.x.w %[Rd], f0\n\t"
"rdcycle t1\n\t"
"sub %[RdC], t1, t0\n\t"
: [Rd] "=r" (f0S.u32Dat.LowW), [RdC] "=r" (nCyc)
: [Rs1] "r" (f1S.u32Dat.LowW), [Rs2] "r" (f2S.u32Dat.LowW), [Rs3] "r" (f3S.u32Dat.LowW)
: "t0", "t1");
Serial.printf("TEST-fmul.s then fadd.s #%u\r\n", tnum);
Serial.printf("CYCLE: %u\r\n", nCyc);
Serial.printf("%f * %f + %f = %f\r\n", f1S.fDat, f2S.fDat, f3S.fDat, f0S.fDat);
Serial.printf("%e * %e + %e = %e\r\n", f1S.fDat, f2S.fDat, f3S.fDat, f0S.fDat);
Serial.printf(" HEX: %08x\r\n", f0S.u32Dat.LowW);
Serial.printf("\r\n");
}
void tst_Fmadd(uint32_t tnum, float arg1, float arg2, float arg3)
{
uint32_t nCyc = 0;
TestFloat f0S, f1S, f2S, f3S;
f0S.fDat = 0.0;
f1S.fDat = arg1;
f2S.fDat = arg2;
f3S.fDat = arg3;
asm volatile("fmv.w.x f0, %[Rd]\n\t"
"fmv.w.x f1, %[Rs1]\n\t"
"fmv.w.x f2, %[Rs2]\n\t"
"fmv.w.x f3, %[Rs3]\n\t"
"rdcycle t0\n\t"
"fmadd.s f0, f1, f2, f3\n\t"
"fmv.x.w %[Rd], f0\n\t"
"rdcycle t1\n\t"
"sub %[RdC], t1, t0\n\t"
: [Rd] "=r" (f0S.u32Dat.LowW), [RdC] "=r" (nCyc)
: [Rs1] "r" (f1S.u32Dat.LowW), [Rs2] "r" (f2S.u32Dat.LowW), [Rs3] "r" (f3S.u32Dat.LowW)
: "t0", "t1");
Serial.printf("TEST-fmadd.s #%u\r\n", tnum);
Serial.printf("CYCLE: %u\r\n", nCyc);
Serial.printf("%f * %f + %f = %f\r\n", f1S.fDat, f2S.fDat, f3S.fDat, f0S.fDat);
Serial.printf("%e * %e + %e = %e\r\n", f1S.fDat, f2S.fDat, f3S.fDat, f0S.fDat);
Serial.printf(" HEX: %08x\r\n", f0S.u32Dat.LowW);
Serial.printf("\r\n");
}
main()関数内に記載のテストケース
テストケースは同じ値をそれぞれの関数に対して与えてみます。数値組は2つなので関数との組み合わせで合計4ケースです。与えている数値は全て10進浮動小数なので「見ればわかる」。
//--- DUT -------------------------------- tst_Fmult_fadd(1, 1.234567, 9.876543, 1.123456); tst_Fmadd( 2, 1.234567, 9.876543, 1.123456); delay(5000); tst_Fmult_fadd(3, 1.234567, 1.134567, 1.123451); tst_Fmadd( 4, 1.234567, 1.134567, 1.123451); //--- END OF DUT--------------------------
実機上での実行結果
それぞれのテストケースの最初に CYCLE: の後にサイクル数の計測結果が記載されています。演算命令の直前から、演算結果を整数レジスタに転送した直後までの「見かけの」サイクル数です。rdcycle命令1個分と、演算結果を整数レジスタへ転送する命令1命令分のサイクル数が含まれます。整数レジスタへの転送の後で測っているのは、整数レジスタに転送するためには浮動小数点演算の結果が出ていないとならないからです。サイクル数を測定したけれど裏でまだ計算していた、といった事態を避ける意図ですが(大丈夫か。)ともかく、#1と#2、#3と#4の結果の差をとると、単純演算2個と積和演算1個の「差分」が求まっている筈。11引く8ですから
3サイクル
であります。積和演算命令1回につき3サイクル「お得」とな。「普通」は何千万回、何億回と繰り返す筈なのでお得感もひとしおかと。
TEST-fmul.s then fadd.s #1 CYCLE: 11 1.234567 * 9.876543 + 1.123456 = 13.316710 1.234567e+00 * 9.876543e+00 + 1.123456e+00 = 1.331671e+01 HEX: 4155113f TEST-fmadd.s #2 CYCLE: 8 1.234567 * 9.876543 + 1.123456 = 13.316710 1.234567e+00 * 9.876543e+00 + 1.123456e+00 = 1.331671e+01 HEX: 4155113f TEST-fmul.s then fadd.s #3 CYCLE: 11 1.234567 * 1.134567 + 1.123451 = 2.524150 1.234567e+00 * 1.134567e+00 + 1.123451e+00 = 2.524150e+00 HEX: 40218bac TEST-fmadd.s #4 CYCLE: 8 1.234567 * 1.134567 + 1.123451 = 2.524150 1.234567e+00 * 1.134567e+00 + 1.123451e+00 = 2.524150e+00 HEX: 40218bad
演算結果は同じものを、%f形式と%e(指数)形式の2通りで表示しています。#1と#2、#3と#4が同じ結果になる筈。10進の浮動小数点数として表示している限りでは違いは見当たりませぬ。しかし、#3と#4の結果の16進表現 HEX: の後の数字をご覧ください。
cとdです。1ビットですが違ってました
これが途中に丸めが入るか、入らないかの微妙な差です。私のようないい加減な年寄りからすると、1ビットくらいいいじゃん、と踏みつぶしたくなるのですが、精度に厳しいお兄様、お姉様におかれましては許せないかもしれません。繰り返しになりますが、何百万回も繰り返す積和算なので、塵も積もれば山となる、と。知らんけど。