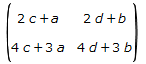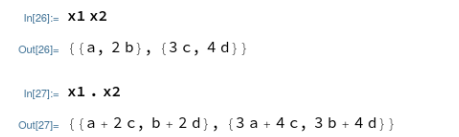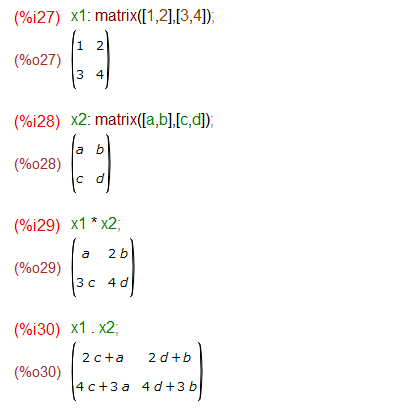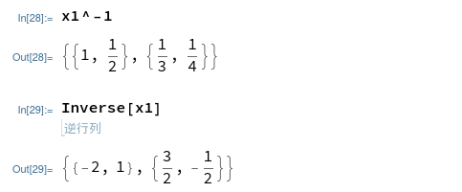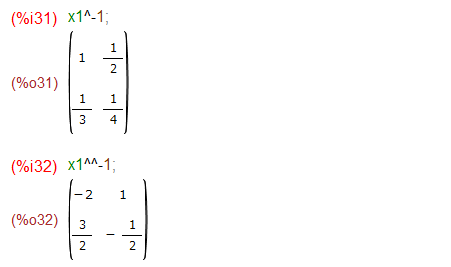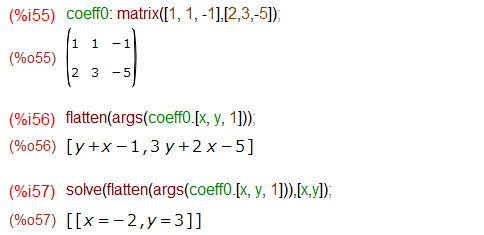今回は線形代数、といっても入り口だけです。行列の記述の方法と演算子の書き方くらいまで。1回やそこらで線形代数が終わる筈はないです。これまた基本のキなのでMathematicaとMaximaに線形代数に関する同様な機能が無い筈ないのです。しかし両者のお家流、似ているようで違ってました。
※「忘却の微分方程式」投稿順 index はこちら
※文中で Maximaとあるのは、MaximaにGUIを被せたwxMaxima 21.05.2 (Windows版)です。Mathematicaはラズパイ上の12.2.0.0です
※学生でもないのに勝手に参照させていただいておりますWolfram社Mathematicaのチュートリアルは以下です。
今回はWolfram社のチュートリアルの題材をMaximaで同様にやるにはどうするか、という感じで行きたいと思います。
行列(Matrix)の実体はどちらもリスト
MathematicaもMaximaも行列の実体は、行ベクトルを列方向にならべたネストしたリストであるようです。しかし「行列として表示する」ところに注目すると以下の違いがあります。
- Mathematicaはネストしたリストを行列として解釈して計算(行列だという指定など不要)
- しかし、そのままでは行列としての表示はされずリストはリストとして表示される(行列表示用の関数に渡すとようやく行列形式で見られる)
一方Maximaの場合、
- 専用の関数matrix()により「行列」という属性のついたリストが作られる
- 行列として計算できることは勿論、何もしなくても行列表示となる
勿論、Mathematicaのリストは中カッコくくり、Maximaは大かっこ(角カッコくくり)が御家流であります。論より証拠、Mathematicaでやってみたところがこちら。
例によってMathematicaには、入力時点から行列風の2次元的並びで記入する方法が用意されてました。CTRL+カンマで列を、CTRL+ENTERで行を入力していくスタイルです。
一方のMaximaの場合がこちら。aの定義では単なるリストのまま、bのように書くと行列という属性が付けられて、行列として表示されます。
行列を作る
単位行列とかアリガチな形の行列を作る機能は当然あるのですが、式を使って行列の要素を生成する例がMathematicaのチュートリアルに載ってました。まあ、リストを作ってそれを行列表示しているだけですが。
同じことを、Maximaの genmatrixという、その名からして行列生成用の関数で行ってみたのが、以下に。
第1引数に生成用の関数をとるので、ここはlambda関数で定義してみたものの、引き続く, x, y の範囲を示す引数の順番が普通と逆じゃないか、と文句を垂れたくなります。順番は x上限、y上限、x下限, y下限です。
CSVファイルからの配列読み込み
MathematicaもMaximaも数値計算向きのソフトではないのですが、外部からデータを取り込んで処理するための機能は一応持っていました。テキストファイルで定番のCSV形式を読み込めるのは当然。とりあえず以下のようなCSVを作って両者に読み込ませてみました。
1,2,3,4 5,6,7,8
まずMathematicaです。何も準備することなく、Inport[]関数一発で、4列2行が読み込まれ、そのままの形でリストになりました。行列に「見せかける」にはMatrixForm[]関数です。
一方Maximaの場合、csv形式の読み取り関数を使うためには、モジュールのロードが必要なようでした。numericalioとな。load()関数でnumericalioモジュールをロードすれば各種関数が使えるようになります。その中にMatrix形式で読み取る関数もありました。「matrixとして」読み込んでいるので何もしなくても行列表示されます。
行列の計算
ここでの考え方は両者似ています。「普通の演算子」類は行列の各要素毎の計算に使う、行列積などの行列独特の処理は、専用の演算子か関数にお願いするというスタイル。
まずはMathematicaから。スペース開けて変数を並べれば掛け算になるので、2x2行列を格納した行列をただ並べると要素毎の掛け算、それにたいして ”.” (ドット演算子)を適用すると行列積となりました。
Maximaの例がこちら。2x2の行列を定義して、要素毎の掛け算には * 、行列の掛け算には “.” (ドット演算子)を使います。
逆行列はチト違いますな。
まずMathematica、普通に-1乗すると要素毎の逆数がとられます。逆行列を得るには、Inverse[]関数にお願いする、と。
Maximaの場合も、普通に-1乗すると要素毎の逆数ですが、逆行列を得るには、”^^” (ダブル・サーカムフレックスとでもいうべきか?)演算子を使うことができます。
行列方程式を解く
行列を使った連立方程式の表現
A . x = b
を解くためにMathematicaには LinearSolve関数がありました。行列Aと列ベクトルbを与えれば、xに当たるお答えを求めてくれます。
勿論、Maximaにも連立方程式を求めるsolve()関数がありますが、こちらは式のセットを与える必用があります。そして式のセットからAにあたる係数行列を取り出す関数などがあります。しかし、上のような係数行列を与えて連立方程式を解くような関数が見当たりませんでした。無理やりやってみたのが以下です。
一応、Aとbを並べた行列を作っておいて行列積をとってから、配列を単純リストにしてフラット化する、という手順で解くことは解ける、と。でもま、普通に連立方程式を与える方が楽な気もしないでもない。