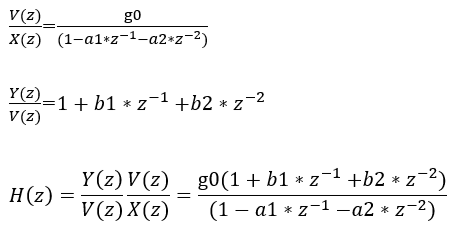前回は周波数シフタの全貌を実機で観察。今回はその構成要素初段のDCカット・フィルタについて調べてみたいです。フィルタのコードはIIRフィルタを「手習ひ」したときに既に使っていたのですが、忘却の彼方。今回はScilab使ってその特性を調べた後、実機でDCカットフィルタを「外したら」どうなるのか観察してみたいと思います。
※「手習ひデジタル信号処理」投稿順 Indexはこちら
以下は、勝手に手習ひさせていただいております教科書へのリンクです。
三上直樹先生著、工学社『「Armマイコン」プログラムで学ぶデジタル信号処理』
上記教科書の6.3「ヒルベルト変換器」による「位相シフタ」を使う「周波数シフタ」のうち「直流分除去フィルタ」が今回のお題であります。なお、三上先生のソースは、Arm社のMbed Webコンパイラ環境(要無料登録)で参照可能です。
DC cut Filter
ここで使われているフィルタのコードはIIRフィルタの基本ブロック1個です。三上先生の教科書付録のIIRフィルタ設計ツールを使い、
-
- 遮断周波数: 50Hz
- バタワース特性の2次の高域通過フィルタ
として係数を設計したもののようです。三上先生ツールは教科書に書いてある合言葉を使わないとダウンロードしても取り出せませんが、そういう設計できるツールは他にもありそうに思います。
さてその差分方程式は以下のようです。
v[n]=a1*v[n-1]+a2*v[n-2]+g0*x[n] y[n]=v[n]+b1*v[n-1]+b2*v[n-2]
上記から伝達関数を求めれば、Scilab様にボード線図を描いてもらえるのです。中学生レベルの式の変形ですが、年寄りにはこれが辛いです。が、Maxima様にお願いすることなく、自力で手計算してみましたぞ(よって間違っているかもしれません。知らんけど。)
こうして伝達関数さえ求まれば、後は機械的にコードすればよろし、と。以下のコード中の係数は三上先生教科書で使われている値です。
// DC cut filter(org: 三上先生)
clc;
clear();
clf();
g0=9.780305e-1
a1=1.955578
a2=-9.565437e-1
b1=-2.0
b2=1.0
Hz = syslin('d', g0*(1+b1*%z^(-1)+b2*%z^(-2))/(1-a1*%z^(-1)-a2*%z^(-2)))
bode(Hz, 0.001, 1.0)
xtitle("DC Cut Filter 正規化周波数 Bode Plot")
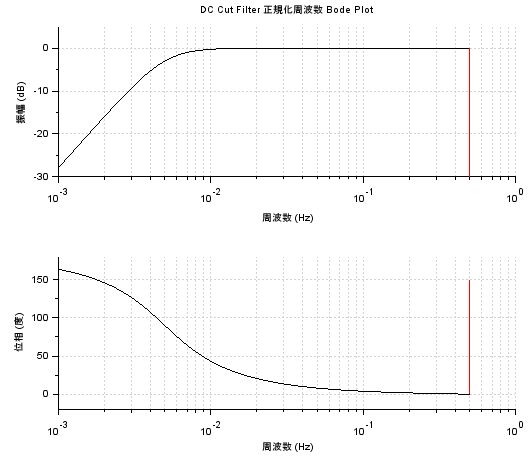
以下がScilab出力のBode線図ですが、デジタルフィルタとて、X軸はサンプリング周波数を1Hzとした「正規化された」周波数で、上限はナイキスト周波数0.5Hzまでのプロットです。今回実機ではサンプリング周波数10kHzなので、以下の赤線が5kHz、10-1が1kHz、10-2が100Hz相当ということになります。
確かにDCに近い低い周波数は抑圧されているようです。
実機でDCカットフィルタのON/OFFの効果を観察
前回、完全なコード(DCカットフィルタが働いている)で波形を観察しているので、今回はその部分を潰して挙動の差をみてみます。以下に示す1箇所をコメントアウトするだけ。Arm MbedのWebコンパイラ環境で作業しているので修正後のビルドも簡単、ほとんど一撃であっという間にオブジェクトが出来上がります。例によってオブジェクトをSTM32F446REにダウンロードすれば実行準備OKです。
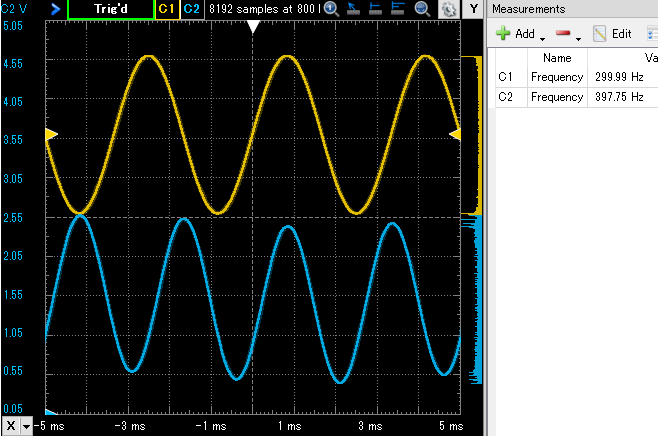
まず、時間波形を観察してみます。前回同様、C1(黄色)の入力に300Hz、振幅1V、オフセット0Vの波形を入れて、C2(青色)の出力をみてみます。予定通り、ほぼ100Hzの周波数シフトが起こっていますが、前回の「完全版」の波形とくらべると波形が「うねっている」感じがします。
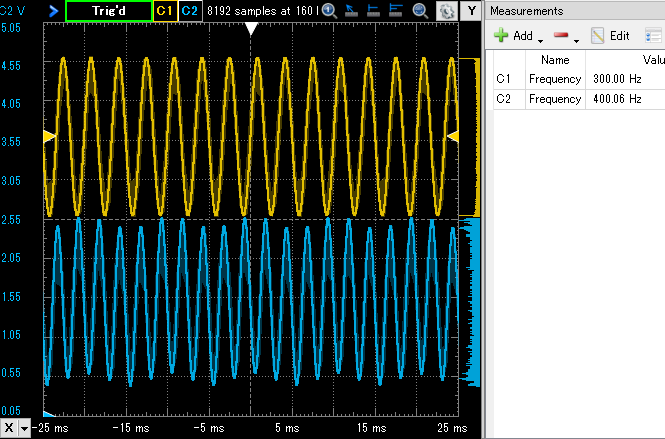
うねっている感じをみるため表示スパンを長くしてみました。こんな感じ。青の出力波形がヒョコヒョコと上へ下へと動いているのが分かります。
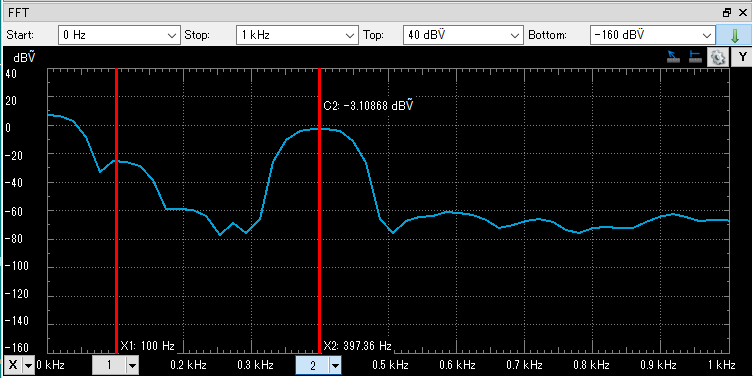
そこでFFTかけてみるとその様子がハッキリします。予定どおり400Hz付近にピークがあるのですが、100Hz(DC成分を100Hzシフトしたら100Hzとなる)あたりにも小山が見えてます。
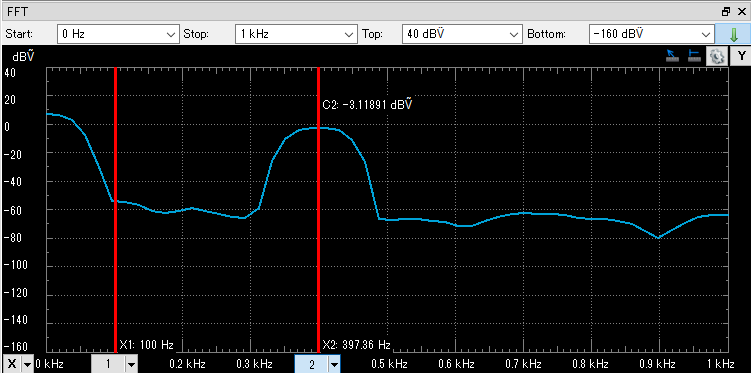
比較のため、前回の「完全版」のオブジェクトコードを走らせたときのFFTの結果を見ると以下のようです。100Hzのところに小山は無いっと。
「デジタル」なだけあって、「計算通り」に動いていてよかった。