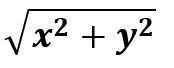加減乗除に最大/最小、比較とやってきましたが、まだ残っている「演算系の浮動小数点命令」がありました。平方根です、Square Root。平方根を計算するだけでは芸が無いので、2次元のnormも計算してみました。x86(というかx87)系のFPU命令であると「超越関数」までありますが、RISC-Vには超越関数不在です。加減乗除とアルゴリズムで後はよしなに、と。
※「ぐだぐだ低レベルプログラミング」投稿順indexはこちら
いや~別件ですが、ルネサスからRISC-V機登場したようです。コアは台湾のAndes Technology設計みたいです。ルネ様のスペック拝見するにRISC-V機としたら現状ハイエンド機ですな。是非とも使ってみたいもんですが、ルネサス製の評価ボードとかそれなりのお値段だろうからなあ、立派だけれどお高い?それに開発ツールが別売だったりもするし。ラズパイと同程度のお値段で手に入ると良いのだけれど。。。
※以下は単精度浮動小数点演算命令について述べています。なお実機動作は、64bit RISC-V搭載、Kendryte K210上で行っています。
単精度浮動小数の平方根命令
レジスタ一つを引数にとり、ルートを計算して結果をレジスタ一つに書き戻します。
fsqrt.s rd, rs1
今回、負の数を引数にとったらどうなるのか調べてないです。メンドイというか忘れました。後で他の件と合わせて扱うかもしれません。
ルートとるだけではあんまりなので、アイキャッチ画像に掲げたとおり、norm計算(2次元ですけれども)をやってみました。以前やりました積和演算命令を使えば、積和して積和して平方根、というシーケンスで計算できます。勿論、3次元以上になったら次元の数だけ積和算を増やせばよい、と。簡単。ホントか。
被テスト関数のソース
ブツブツいいながらも、「定形」コピペで追加です。fsqrt.s単独テスト用とnorm計算用の2種。今回は実行サイクル数の計測も含めましたです。
void tst_Fsqrt(uint32_t tnum, float arg1)
{
uint32_t nCyc = 0;
TestFloat f0S, f1S;
f0S.fDat = 0.0;
f1S.fDat = arg1;
asm volatile("fmv.w.x f0, %[Rd]\n\t"
"fmv.w.x f1, %[Rs1]\n\t"
"rdcycle t0\n\t"
"fsqrt.s f0, f1\n\t"
"fmv.x.w %[Rd], f0\n\t"
"rdcycle t1\n\t"
"sub %[RdC], t1, t0\n\t"
: [Rd] "=r" (f0S.u32Dat.LowW), [RdC] "=r" (nCyc)
: [Rs1] "r" (f1S.u32Dat.LowW)
: "t0", "t1");
Serial.printf("TEST-fsqrt.s #%u\r\n", tnum);
Serial.printf("CYCLE: %u\r\n", nCyc);
Serial.printf("%f <- fsqrt.s(%f)\r\n", f0S.fDat, f1S.fDat);
Serial.printf("%e <- fsqrt.s(%e)\r\n", f0S.fDat, f1S.fDat);
Serial.printf(" arg1 HEX: %08x\r\n", f1S.u32Dat.LowW);
Serial.printf("\r\n");
}
void tst_Fnorm(uint32_t tnum, float arg1, float arg2)
{
uint32_t nCyc = 0;
TestFloat f0S, f1S, f2S;
f0S.fDat = 0.0;
f1S.fDat = arg1;
f2S.fDat = arg2;
asm volatile("fmv.w.x f0, %[Rd]\n\t"
"fmv.w.x f1, %[Rs1]\n\t"
"fmv.w.x f2, %[Rs2]\n\t"
"rdcycle t0\n\t"
"fmadd.s f0, f2, f2, f0\n\t"
"fmadd.s f0, f1, f1, f0\n\t"
"fsqrt.s f0, f0\n\t"
"fmv.x.w %[Rd], f0\n\t"
"rdcycle t1\n\t"
"sub %[RdC], t1, t0\n\t"
: [Rd] "=r" (f0S.u32Dat.LowW), [RdC] "=r" (nCyc)
: [Rs1] "r" (f1S.u32Dat.LowW), [Rs2] "r" (f2S.u32Dat.LowW)
: "t0", "t1");
Serial.printf("TEST-fnorm.s #%u\r\n", tnum);
Serial.printf("CYCLE: %u\r\n", nCyc);
Serial.printf("%f <- norm(%f, %f)\r\n", f0S.fDat, f1S.fDat, f2S.fDat);
Serial.printf("%e <- norm(%e, %e)\r\n", f0S.fDat, f1S.fDat, f2S.fDat);
Serial.printf(" arg1 HEX: %08x\r\n", f1S.u32Dat.LowW);
Serial.printf(" arg2 HEX: %08x\r\n", f2S.u32Dat.LowW);
Serial.printf("\r\n");
}
テストケース
今回のテストケースは以下ですが、「ベタ」なものばかり。
-
- ルート2、ひとよひとよにひとみごろ
- ルート3、ひとなみにおごれや
- ピタゴラスの定理、古代メソポタミア以来の3,4,5!
遥かな太古の時代、中学の数学の先生に「ひとよひとよにひとみごろ」みたいなことを習ったような気がします。最近はそんな語呂合わせはしないのかな。スマホで一発。でも平方根は、開平すれば手計算でも求まるのだけれど。開平こそ今時計算しないか。だいたい手計算ができずにMaxima様にお願いしている自分が何を言う。
tst_Fsqrt(0, 2.0f); tst_Fsqrt(1, 3.0f); tst_Fnorm(2, 3.0f, 4.0f);
実機上での実行結果
実機上での実行結果は、予定どおりでありますな。単精度浮動小数点数なので、桁数的に語呂合わせより短いッスけど。normも、ちゃんと三平方の定理の代表例どおりみたいだし。
TEST-fsqrt.s #0 CYCLE: 32 1.414214 <- fsqrt.s(2.000000) 1.414214e+00 <- fsqrt.s(2.000000e+00) arg1 HEX: 40000000 TEST-fsqrt.s #1 CYCLE: 32 1.732051 <- fsqrt.s(3.000000) 1.732051e+00 <- fsqrt.s(3.000000e+00) arg1 HEX: 40400000 TEST-fnorm.s #2 CYCLE: 41 5.000000 <- norm(3.000000, 4.000000) 5.000000e+00 <- norm(3.000000e+00, 4.000000e+00) arg1 HEX: 40400000 arg2 HEX: 40800000
平方根、計算できるですね。よかった。何が?