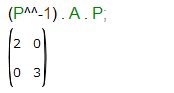このシリーズ、1か月ほど間が空いてしまいました。老人の忘却力とて、1か月もお休みするとMaximaの使い方も危ないです。か細い記憶をたどりつつ、前回の流れで今回は固有値と固有ベクトルの計算、そして対角化へと入っていきとうございます。みんな大好き P-1AP ってやつ?
※「忘却の微分方程式」投稿順 index はこちら
※以下の参考書(以下URLは「改訂9」)の「改訂1」版の演習問題をMaximaの練習用に使わせていただいております。
数学の御本なのに数学の勉強には全然なってないです。恐れ多いことです。すみません。
行列の固有値、固有ベクトルを求める
Maxima様におかれましては 2×2 だろうが、 3×3 だろうが気にすることもないのでありますが、「人力」で解く(勉強する)教科書ではまずは 2×2 サイズで固有値や固有ベクトルを求めてます。まあ、Maximaにお願いしてみるとこんな感じ。
eigenvalues()に行列を渡せば固有値が、eigenvectors()では固有ベクトルが返ってくるのですが、かえってくるリストの形式がチト?です。まず、eigenvalues(A)の方をみると、2重のリストです。
[[3,2],[1,1]]
ここで外側のリストの第1要素のリスト [3,2] こそが固有値のリストで、第2要素 [1,1] の方はそれぞれの固有値に対応する重複度のリストみたいです。ことさらに重複度を入れて固有方程式を書き表すと以下のようである、ということで良いですかね。ホントか?
(λ1-3)^(1)*(λ2-2)^(1)=0
さて次にeigenvectors(A)を見てみるとこちらは3重のリストです。外側のリストの第一要素は、先ほどの eigenvalues(A)そのもののようです。eigenvectors使えば、eigenvalues使う必要は無かったのね。。。
第2要素が固有値ベクトルのリストのようです。ただ、上記の戻り値の表記法はリストになっています。この場合、多分、数学で一般的な列ベクトル表記ではないです。上手いやり方を思いつかなかったので、力ずくで上記の形式の固有ベクトル2個を列ベクトル表記に直してみました。こんな感じ。
固有ベクトル2つ、X1とX2が求まったのでこれを「ならべて」変換行列Pを作り、Pの逆行列PIと、PでAを挟み込んで P-1AP してみたいと思います。固有ベクトルは適当にスカラー倍して順番変えてますけれども、これは教科書と同じ形にしたかったための操作です。こんな感じ。
P-1APできました。これで行列Aが対角行列に変換できた、と。なお、冒頭のアイキャッチ画像にも掲げましたが、逆行列は Intert(P) でなく、P^^-1 としても求まります(ご存じのとおり、P^-1とすると要素毎に逆数がとられます。)
以下はついでです。Maximaには特性多項式(固有多項式)求めるcharpoly()関数もありました。実際行列Aに適用してみると以下のようです。そして求めた特性多項式をsolveに渡してやれば、ちゃんと固有値求まっているようです。
今回はリハビリ編ですかね。毎回少しお休みする度にリハビリしていたら先に進むどころか退化しそうだけれども。老人の忘却力は凄いのよ。