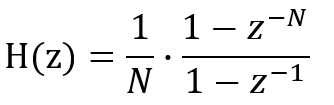前回は教科書のプログラムをそのまま実機STM32F446REマイコン上に実装、CICフィルタのON/OFFでどのような特性になるのか観察いたしました。今回はそのCICフィルタの振幅特性をScilabを使って計算してみたいと思います。前回使用したCICフィルタは３段の継続接続であったので、１段から３段まで比較してみます。
※「手習ひデジタル信号処理」投稿順 Indexはこちら
※参照させていただいております三上直樹先生著の教科書は以下です。
工学社『「Armマイコン」プログラムで学ぶデジタル信号処理』
前回使用させていただいていた三上先生の御ソースは、Arm社のMbedのWeb環境（要登録、無料）内で公開されており、「呂」で検索すれば発見できます。
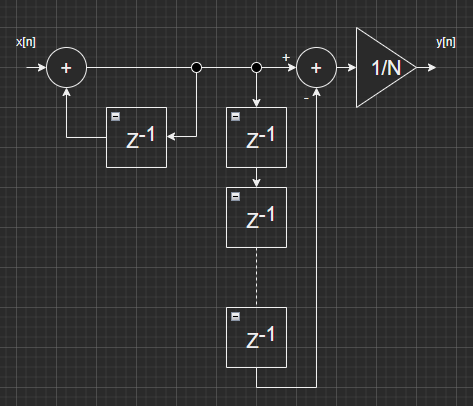
CIC(Cascaded Integrator-Comb)フィルタ１段分のブロック図
ボーっとして生きているので、今回使用のCICフィルタと同じものを以前に実習していたことを忘れていました。同様な構成のフィルタを第８回で使用してました。今回使用のフィルタは以下の図でN＝５のときです。
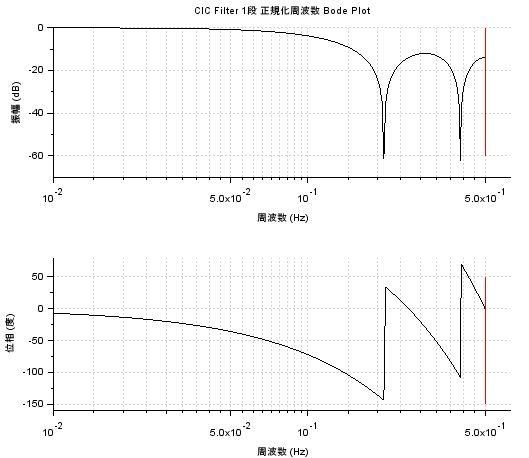
１段分の伝達関数とそのボーデ線図
上記ブロック図のフィルタの１段分の伝達関数が以下に。
上記の伝達関数の振幅特性を求めるためのScilabプログラムが以下です。
// CIC filter 1段
clc;
clear();
clf();
N=5
Hz = syslin('d', (1/N)*(1-%z^(-N))/(1-%z^-1))
bode(Hz, 0.01, 1.0)
xtitle("CIC Filter 1段 正規化周波数 Bode Plot")
例によって、上のプログラムからはサンプリング周波数を1Hzとして正規化したボード線図が得られます。プロットはナイキスト周波数となる0.5Hzまでとなります（グラフの赤の縦棒。）1段ではちょっと十分ではない、と。
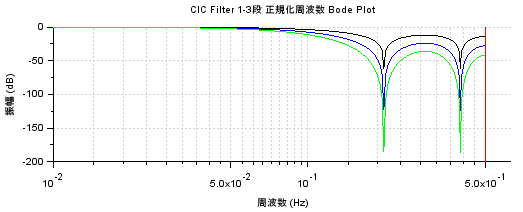
１～３段の継続接続の場合の振幅特性を重ねてプロット
１，２，３段の振幅特性を重ねてプロットするためのScilabプログラムが以下に。
// CIC filter 1,2,3段
clc;
clear();
clf();
N=5
Hz1 = syslin('d', (1/N)*(1-%z^(-N))/(1-%z^-1))
Hz2 = syslin('d', ((1/N)*(1-%z^(-N))/(1-%z^-1))^2)
Hz3 = syslin('d', ((1/N)*(1-%z^(-N))/(1-%z^-1))^3)
bode([Hz1; Hz2; Hz3], 0.01, 1.0,['1段','2段','3段'])
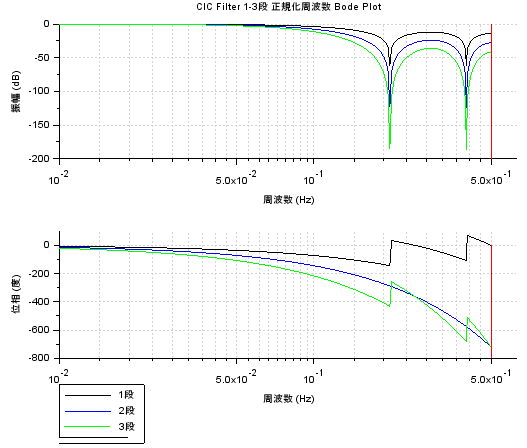
xtitle("CIC Filter 1-3段 正規化周波数 Bode Plot")
その計算結果が以下です。やはりサンプリング周波数を1Hzとして正規化したボード線図です。黒が１段、青が２段の継続接続、黄緑が３段の継続接続の時です。段数深くなるにつれ特性が良くなってます。前回実機上で利用したの３段継続接続でした。実機上のナイキスト周波数は5kHzであったので、2kHz付近の「問題の」信号を強力に抑制してくれそうな感じです。知らんけど。
CICフィルタ分かった気がします。いや、それ誤解だから。