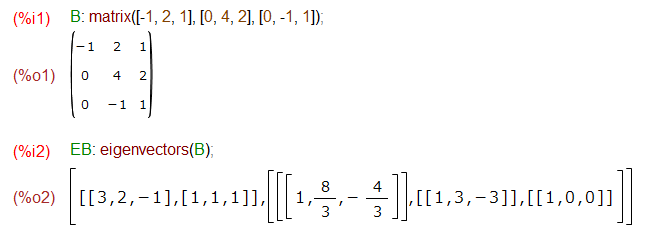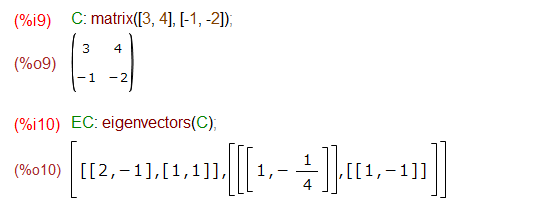前回、みんな大好き P-1AP ってやつまでたどり着いていたので、今回は単純な計算練習のつもり。練習っていって計算するのはMaxima様ですが。けれど単純に以下同文できないところが用意されとりました。「固有値が重解を持つ場合でも、対角化可能なものもある」と。勿論、対角化可能でないものもあるっと。恐れ入ります。
※「忘却の微分方程式」投稿順 index はこちら
※以下の参考書（以下URLは「改訂９」）の「改訂１」版の演習問題をMaximaの練習用に使わせていただいております。
数学の御本なのに数学の勉強には全然なってないです。恐れ多いことです。
計算練習：３ｘ３行列の変換行列を用いた対角化
前回やった事に準じて作成した手順が以下に。Pの作成のところがチト順番やらスカラー倍やらしているのは教科書と「バッチリ」な途中経過にするためのお化粧であります。
B: matrix([-1, 2, 1], [0, 4, 2], [0, -1, 1]) EB: eigenvectors(B) X1: transpose(EB[2][1][1]) X2: transpose(EB[2][2][1]) X3: transpose(EB[2][3][1]) P: addcol(X3, X2, 3*X1) PI: invert(P) PI . B . P
まずは固有ベクトルを求めたところが以下に。
リスト形式の固有ベクトルから列ベクトル形式での取り出し。列ベクトルを並べて変換行列Pを作るところまで。
変換行列Pが出来たので、 P-1AP して対角化っと。
対角化できたようです。これなら、この手順のまま関数にしてしまいたいくらい。でも大丈夫か？
計算練習：２ｘ２行列の変換行列を用いた対角化
一歩もどって、２ｘ２行列の場合の計算問題が以下に。以下同文的に解いてみます。
C: matrix([3, 4], [-1, -2]) EC: eigenvectors(C) X1: transpose(EC[2][1][1]) X2: transpose(EC[2][2][1]) P: addcol(4*X1, X2) PI: invert(P) (P^^-1) . C . P
まずは固有ベクトルを求め、
列ベクトルを取り出して、
変換行列を作って、 P-1AP。
対角化できましたな。
計算練習：３ｘ３行列の変換行列を用いた対角化、問題の件
同様に３ｘ３行列ですが、以下はちょっとトラブった件。
D: matrix([2, 1, 0], [1, 2, 0], [1, 1, 1]) ED: eigenvectors(D) X1: transpose(ED[2][1][1]) X2: transpose(ED[2][2][1]) X3: transpose(ED[2][2][2]) P: addcol(X2, X3, X1) (P^^-1) . D . P
ぼーっとして生きているので、以下の固有値、固有ベクトルのお答えがちょいと違うのを最初は見逃してます。
いつもの手順で列ベクトルを取り出そうとして、エラーに遭遇しました。こんな感じ。
これは、eigenvectors()の返り値を見れば分かるのですが、固有値が重解でした。ただ、その固有値に対応するベクトルはというと線形独立な２つのベクトルが得られていました。
列ベクトルの「抽出」の指定方法を変更して、抽出しなおし、変換行列を作って、 P-1APしてみます。
対角化できました。でも、固有値が重解のとき、いつでも線形独立なベクトルが得られると思うなよ、と。ダメなこともあるのだ、と。