
今回から参照させていただいております教科書は新たな単元?「計量線形空間」に入ります。内積が定義できないとダメなのね。Maximaでベクトルを計算するときはリスト(行ベクトル)をベクトルとみなして計算OK。でも数学の教科書的にはベクトルといったら列ベクトル表記じゃん。そゆときはどうなの?
※「忘却の微分方程式」投稿順 index はこちら
※以下の実習?は、WindowsPC上の以下のバージョンで行わせていただいております。
-
- wxMaxima 21.05.2 (MaximaのGUIフロントエンド的なもの?)
- Maxima 5.45.1
※以下の参考書(以下URLは「改訂9」)の「改訂1」版の演習問題をMaximaの練習用に使わせていただいております。
数学の御本なのに数学の勉強には全然なってないです。恐れ多いことです。
リスト形式のベクトルの内積、なす角
Maximaでは、[1, 2] てな具合に、中カッコで括ることでリストにできます。このリスト形式はベクトルとみなすことが出来て、各種ベクトルの計算OKと。以下の記事でもやっております。
第30回 ベクトル解析その1、MathematicaとMaxima
課題『2つの4次元ベクトルの「なす角」を求めよ』ということで、まずは上記の復習、「リスト形式(行ベクトル)」でやってみます。
上記のとおり、リスト形式では . (ピリオド)演算子で内積がとれます。そこで内積使ってノルムの定義も上記のようにできます。
ノルムと内積が求められるので、以下のように「なす角」を求める関数を定義できました。これを使えば2つのリスト形式の4次元ベクトルのなす角がもとまります。
列ベクトル形式のベクトルの内積、なす角
しかし、数学の教科書でベクトルといえば「列ベクトル」であります。Maximaで列ベクトルを直接入力するのはカッコだらけになってちょいとメンドイです。そこでリスト形式からtranspose()を通して列ベクトル化。列ベクトル化した2つのベクトルを ピリオド演算子で計算してみました。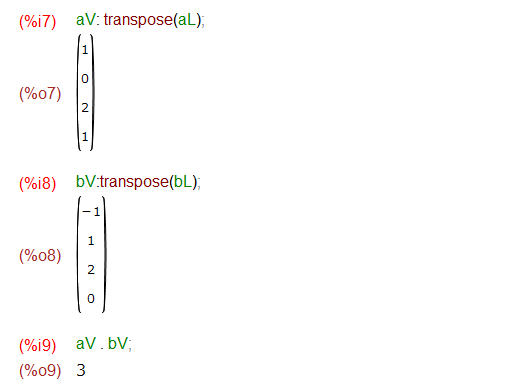
なんだ、普通に内積が計算できているじゃん。それであればリスト形式用に定義してあったノルム計算関数 normL() も使えるんじゃね?
普通に計算できますな。List用だから normL などとLを付けたのは余分だったです。
これまたちゃんと計算できてますな。
リスト形式だろうと、列ベクトルだろうとどんとこい!と
ホント?大丈夫なのね。案ずるより産むがやすしというやつ、違うか。

