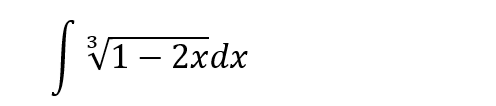今回から積分に入ります。一年近く前に一度、第２５回で積分やっているので復習という感じです。しかし、その時は練習量が少なかったからな～ 分量やらないと。といって実際に汗を流して（流さないか）答えを出してくれるのはMaxima様です。ワタシはMaxima様への「お願いの仕方」を学んでいるだけなのだけれども。
※２０２２年１１月２２日修正：「不定積分」とすべきタイトルが「定積分」となっておりました。お詫びして訂正させていただきます。いよいよ忘却力はなはだし、認知能力低下。
※「忘却の微分方程式」投稿順 index はこちら
※数学のお勉強のための以下の教科書（参考書、問題集？）の例題をMaximaの練習に使わせていただいております。
大昔、大学生のときにこういう御本が欲しかったです。
※以下のMaxima/wxMaximaバージョンで実習させていただいております。
-
- Maxima 5.46.0
- wxMaxima 22.04.0
不定積分その１
今回から積分といって、定石どおり最初は不定積分です。integrate()関数に、被積分関数と、変数を渡してやれば不定積分してくれます。忘却力でもこのくらいは覚えてるんだ（自慢するほどのものでなし。）
上記 %i1 のようにシングルクウォートで評価を抑止すれば積分記号を使って「積分」を表現できるし、%i2 のように評価すれば定積分が求まると。ただし、上でオレンジ色の手書きで付け加えてみた「Ｃは積分定数」というお決まりの「Ｃ」（任意の定数）、Maxima様は省略してしまうみたいデス。必要な人は自分でつけろということ？
続いての例題は３乗根の積分です。こんな感じ。
Maximaの場合、sqrt()関数を使えば平方根は「根号」をつかった表記ができますが、３乗根を上のように表現する方法がわかりません。べき乗を使えば以下のように簡単に表現できますが、美的にはな～。数学できないのに美観にこだわるなよ、自分。
例によってCは省略です。
まあ、この程度の積分であれば問題ないけれど、複雑な積分になったら
積分結果を微分して元に戻るか検算
するのが以前積分をしたときのTIPS？です。内部でいろいろテク使っているらしい積分よりも、機械的に計算できる微分の方が「信用」できるからみたいっす。知らんけど。
次は原始関数にLOGでてくる奴ね。
公式通りといえばそうなのだけれど。
次は自然対数の底 e が出てくる奴。Maxima様の表記法、%e は単なる文字変数 e との区別のためにはやむを得ないとは思うのですが、なんだかな～、美しさにかけるような気がしないでもないデス。まだ言うか、自分。
ついでにもう一題。
まあ、このくらいだと integrate()にお任せするだけなので、苦労はないな～（苦労しているのはMaximaの中の人？だけれども）