前回入力信号を生成する関数群を作成してみました。前々回に時間領域で離散時間っぽいプロットはできるようになってます。今回は、周波数領域でプロットする関数です。Scilabには部品となる関数は用意されているのですが、これ使えばいい的なものはないみたいっす。目標はAnalog Dicovery2の周波数プロット画面ですが。
※「手習ひデジタル信号処理」投稿順 Indexはこちら
※実習に使わせていただいている Scilab処理系は 6.1.1 (Windows版)です。
一度にAnalog Dicovery2の周波数解析画面のようなものを作ろうなどとは、信号処理素人には過ぎたる重荷なので、できるところから細かく刻んでいきたいと思います。大丈夫か?自分。
参照させていただく日本語ドキュメントはしっかりあります。以下は日本語版のヘルプのFFTの項ですが、下の方をみると周波数プロットの例も掲載されており、大変参考になります。
Scilabヘルプ >> Signal Processing > Transforms > fft
また先達が立派な記事をWeb上で公開してくださっています。以下の記事も勉強させていただきました。ありがとうございます。
tera-technology様、ScilabでFFT(前編)、ScilabでFFT(後編)
たけうち成長?日記様 scilab講座その2 フーリエ変換を行う
FFTプロット関数、とりあえず版
「とりあえず版」は、サンプリング周波数[Hz]と、1次元の時間波形(2のべき乗のサンプル数のFFTかけやすいやつ)、オプション一つ、1ならハミング窓、0なら窓無、という関数です。
あとでいろいろ機能強化したいと思いつつ、まずはこれが動作している雰囲気がでているのを確かめるのが今回の目標っす。
// FFT plot
// Fs: sampling frequency [Hz]
// wav: time domain seq(nSample)
// opt: Window function 0:none, 1:hamming
function plotFFT(Fs, wav, opt)
N = size(wav, '*');
regN = 2/N;
select opt
case 1 then
winf = window('hm',N);
regF = 2;
else
winf = ones(1,N);
regF = 1;
end
y = fft(wav .* winf);
xf = Fs*(0:(N/2))/N; //associated frequency vector
nf = size(xf, '*');
clf();
plot2d(xf, abs(y(1:nf)) * regN * regF);
xtitle('FFT', '[Hz]');
endfunction
動作確認
上記をexecしてplotFFT関数を定義しました。また前回作成済の入力波形生成用のgenSin関数もとりこみました。
genSinをつかって、今回プロットするターゲットの波形を生成します。10000Hzサンプリング周波数、4096点、振幅1、位相0度の正弦波波形を2つ足し合わせたものです。周波数は440Hzと555Hz。
信号を生成し、足し合わせ、時間領域と周波数領域でプロットしてみるコードが以下に。
[t, y440]=genSin(10000, 4096, 440, 0, 1); [t, y555]=genSin(10000, 4096, 555, 0, 1); wavT = y440 + y555; plot2d3(t, wavT); plotFFT(10000, wavT, 0); plotFFT(10000, wavT, 1);
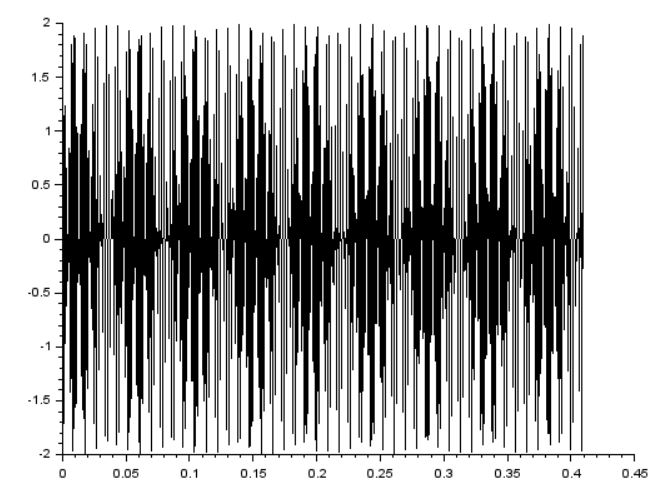
まずはplot2d3で「離散時間」信号っぽく元の波形をプロットとしてみたものが以下に。うねっているような感じ。ホントか?
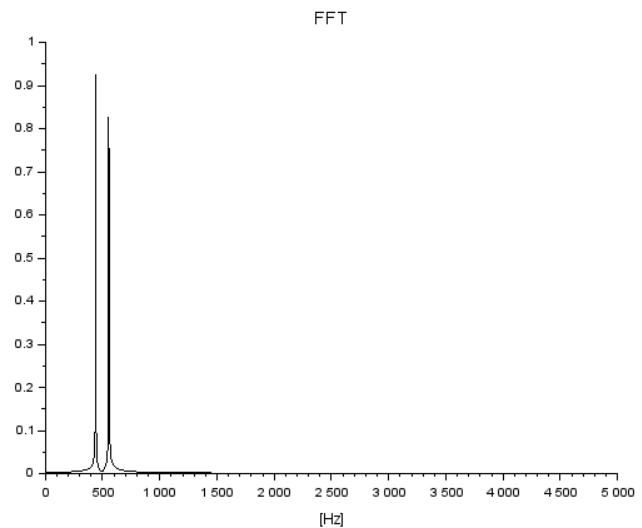
さて本題のplotFFT、まずは窓関数無オプションでのプロット。
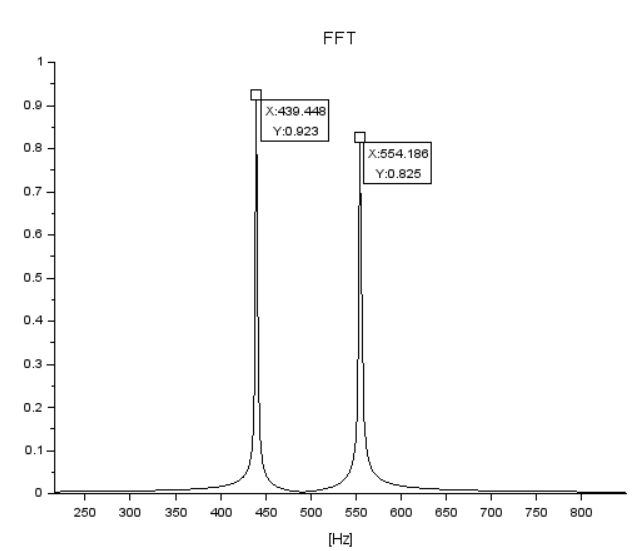
上のグラフだと440Hz付近と550Hz付近にピークがあるのは分かるけれども、見ずらいので拡大してみたものが以下に。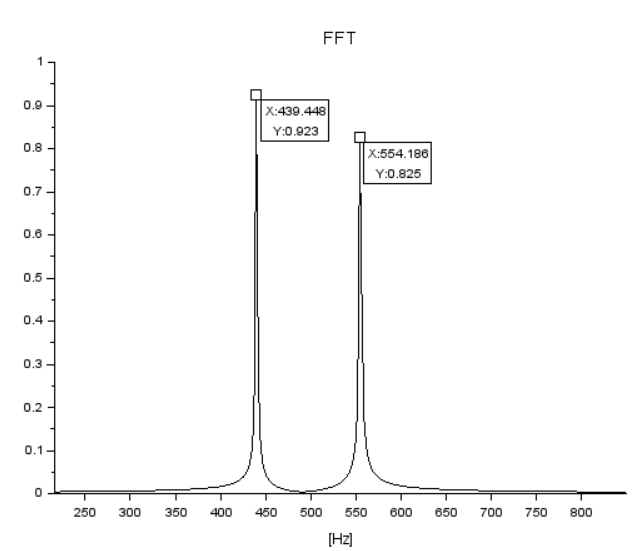
ピークの周波数的には440Hzと555Hzらしいのだけれど、すこし「裾野」が広がってないかい?やっぱり窓関数無にデータを「ぱっつん」しているから?
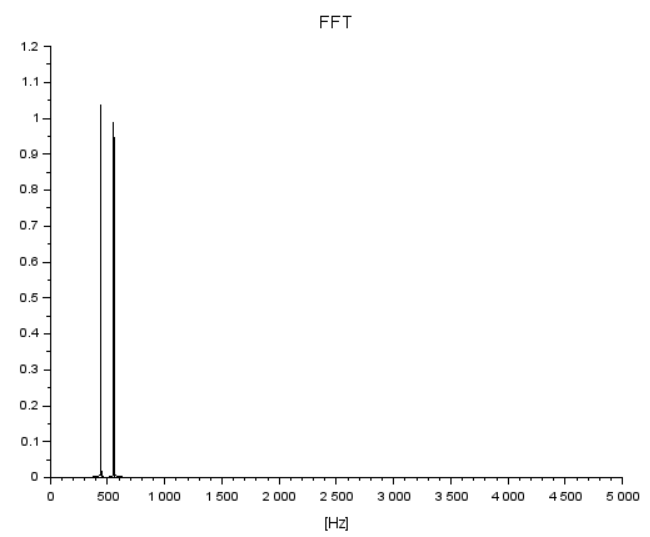
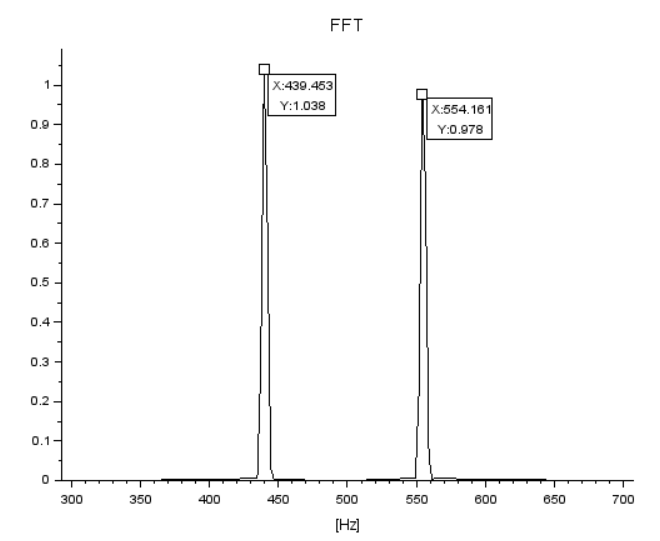
つついて今のところ唯一使えるハミング窓指定の結果が以下に。
たしかに、裾野が狭くなったような気がしないこともない。拡大したものが以下に。
窓関数が効いたのではないかい。知らんけど。