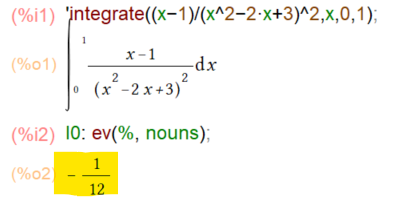今回も定積分の練習をつづけてますが、微妙に一歩進歩したかもしれないです。何度か整理に困っていたlogの引き算を割り算に整理する方法を見つけました。といってマニュアルを読めばわかるのですが。しかし、結果は微妙。も少し工夫しないと数学の宿題的にはマズイです。ま、微妙な一歩でも前進は前進?ホントか?
※「忘却の微分方程式」投稿順 index はこちら
※数学のお勉強のための以下の教科書(参考書、問題集?)の例題をMaximaの練習に使わせていただいております。
大昔、大学生のときにこういう御本が欲しかったです。
※以下のMaxima/wxMaximaバージョンで実習させていただいております。
-
- Maxima 5.46.0
- wxMaxima 22.04.0
さて、もっと以前に読んでおけばよかったMaximaのマニュアル(日本語)ページが以下です。
上記のlogのところに今回の「微妙な一歩」の関数の説明が含まれとります。
例題その1
今回は教科書的には「置換積分」を駆使して積分をもとめよ、という趣旨の例題みたいです。でもMaxima様のやり方にあれこれ文句をつけることは必要ありませぬ(つけろといってもできないケド。)こんな感じ。
デフォルト設定のまま、OKな形で出力されました。よかった。
例題その2
これまたintegrate関数にお願いするだけです。
一撃だな。おい。
例題その3
デフォルトの順番であると、xの2乗の項が後ろへ行ってしまうのがちと見ずらい例題その3です。多分、制御する方法はあるような気がするのだけれど、今は不明。
これまた一発でお答えが。つまらん?
例題その4
ようやく「問題が提起」される例題にたどり着きました。自然対数の底 e が%eという表記になってしまうのでイマイチ美しくない(文句を言うな)以下の定積分であります。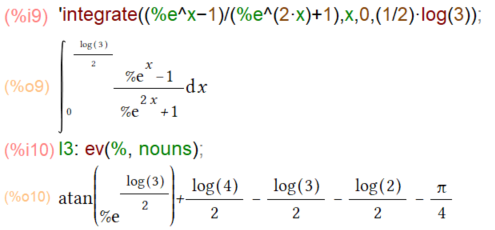
上記のように、定積分の結果は「数値」で得られてますが、未整理。このままでは数学の宿題的にはマズイっす。
そこで例のごとく、radcan()に上記の値 I3 を渡して整理してもらいます。結果は以下に。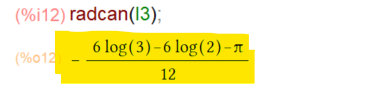
ただね、教科書的には、logの引き算のところを割り算にして、以下のように変形したものをお答えとしとうございます。以前からみたように、radcanは割り算を引き算にする方向への変形はできますが逆はできないようです。
まあ、上の黄色のマーカみたいな結果にしたいです。
とうとう見つけましたぞ、logcontract関数。radcanの逆で、logの引き算を割り算にする方向にまとめてくれるもの。こんな感じ。
しかし、logcontract()を使ってみると以下のようになってしまいました。
頭のボケたこの年寄は電卓たたかないとダメですが、よゐこはお分かりのとおり、729分の64は、3の6乗分の2の6乗であるので、-6*log(3/2)のハズ。「形はまとまって」いるものの、なんだかな~、まとまり過ぎ。先に係数のところだけくくりだしておいてlogの中はシンプルにまとめたかったな~。うまく行かんものです。も少し整理の技を練習しないと。トホホ。