前回は差分方程式をループで回すという「原始的」な方法で1次のIIRフィルタの時間応答を計算してみました。今回はScilabのネイティブ機能を使って、100次のFIRフィルタの応答を「1撃」で計算してみたいと思います。100次のフィルタの係数の計算もScilabに「お任せ」。中身はよくわからないけれど楽ちん。いいのか?
※「手習ひデジタル信号処理」投稿順 Indexはこちら
参照させていただいているScilabの日本語版HELPページ
以下のページに「FIRローパスフィルタの係数」を求めるための関数 ffilt についての説明があります。
ローパスフィルタとタイトルにありますが、ローパス、ハイパス、バンドパス、バンドストップ、皆計算できる関数です。今回はローパスのみ使用してみました。
以下のページではデジタルフィルタの係数を入力信号ベクトル(時系列信号)に適用し出力信号ベクトルを計算してくれる filter 関数が説明されてます。
与える係数は「直接型 II 転置」配置であるようです。「直接型 II 転置」配置は「一番よくつかわれている」のではないかと勝手に想像しています。知らんけど。まあ信号処理プロの人がいろいろ書いてくれてそうです。
filter関数の方は「直接型 II 転置」配置であれば、FIRでもIIRでも適用可能だと思います。
FIRフィルタ関数に一枚かぶせる
上記の係数算出用関数は 正規化された周波数に対して動作するみたいです。正規化周波数のままでは年寄にはイメージが湧かないというとぼけた理由で、このところサンプリング周波数Fsを与える関数を自前作成しています。ffiltにも一枚かぶせてみました(割り算ひとつだけれども。)
作製した関数が以下に。
// Calculate FIR Lowpass Filter
// Fs: sampling frequency [Hz]
// nFlt: number of filter order
// Fc: cutoff frequency [Hz]
function coeff=genFIRLP(Fs, nFlt, Fc)
Fcnorm = Fc / Fs;
coeff = ffilt("lp", nFlt, Fcnorm);
endfunction
実際にフィルタを作成する準備
上記の関数に加えて、過去回で作成した、サンプル波形の作成関数、Fsに対応したFFTのプロット関数などをロードしておきます。以下は、それらスクリプトがHOMEディレクトリ配下のscilabに格納されている場合の例であります。
exec('scilab\genSin.sce');
exec('scilab\genImpluse.sce');
exec('scilab\plotFFT.sce');
exec('scilab\genFIRLP.sce');
FIRローパス・フィルタの作成
今回はサンプリング周波数10kHz、ローパスフィルタの遮断周波数500Hz、FIRフィルタ次数100ということで生成してみました。
Fs=10000; coeff = genFIRLP(Fs, 100, 500);
前回まで1次のフィルタだったのに100次とは一気だな。ま、計算しているのはScilab様だし。
正弦波波形をフィルタしてみる
正弦波2つ、周波数333Hz(遮断周波数より低い)と777Hz(遮断周波数より高い)を重ねた信号を入力信号xとして、これに上記で生成したフィルタをかけて出力信号yを生成してみます。出力信号x, y をFFTにかけて観察すれば、フィルタが働いているか否かが一目瞭然と。
[t, x333] = genSin(Fs, 4096, 333, 0, 1);
[t, x777] = genSin(Fs, 4096, 777, 0, 1);
x = x333 + x777;
[y, zf] = filter(coeff, [1], x);
plotFFT(Fs, x, 1);
xtitle("Input Signal 333Hz + 777Hz, FFT");
plotFFT(Fs, y, 1);
xtitle("Output Signal 333Hz + 777Hz, FFT");
入力 x にFFTかけたものが以下に(プロットはナイキスト周波数5kHzまでなので該当するあたりを手動で拡大してます。)333Hzと777Hzあたりに元気にピークがでております。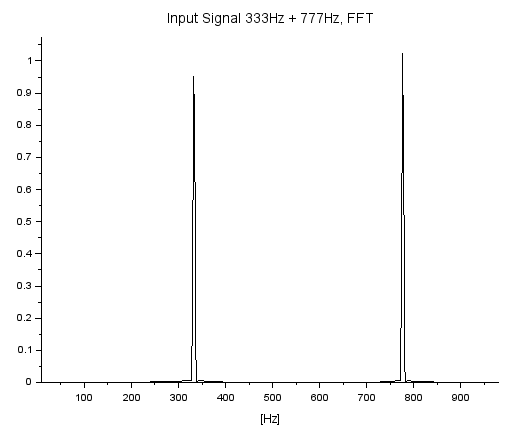
出力 y にFFTかけたものが以下に(プロットはナイキスト周波数5kHzまでなので該当するあたりを手動で拡大してます。)あわれ777Hzは風前の灯状態、一方333Hzは元気。あたりまえか。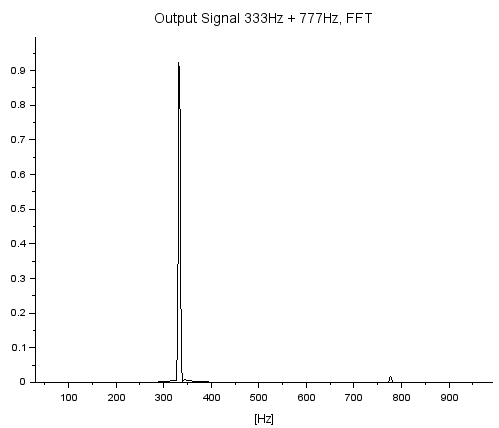
作製したフィルタのインパルス応答(周波数応答)
上記の正弦波波形で雰囲気は分かった(ホントか?)ので、今度はインパルス波形(といってもピークの値1)を作成したフィルタにかけてFFTしてみました。これで周波数応答が求まるハズ。
[ti, xi] = genImpulse(Fs, 4096, 2047, 1);
[yi, zfi] = filter(coeff, [1], xi);
plotFFT(Fs, yi, 1);
xtitle("Impluse response, FFT");
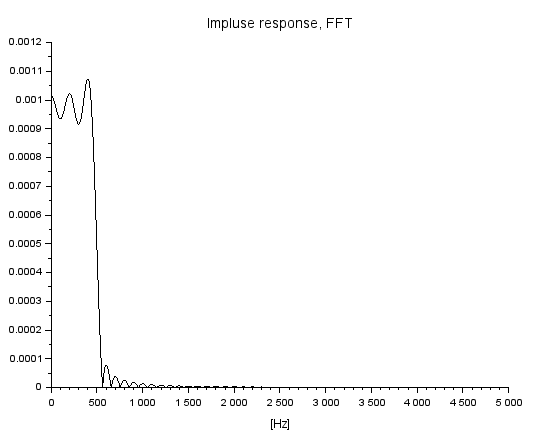
単位インパルス応答の結果が以下に。500Hzでスッパリと切れてるみたいっす。でも縦軸dBじゃない、リニアだあ。またもや後の祭り。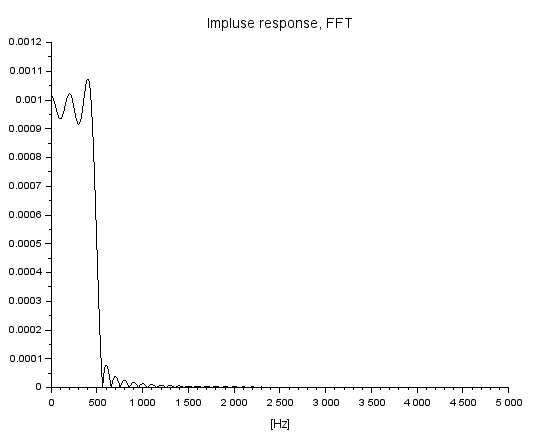
ローパスしているみたいっす。