前回も回転体の体積の定積分でしたが、今回も回転体です。ただし求積法がちょいと異なります。バームクーヘン型とな。バームクーヘンが薄い生地を巻き付けるような構造をしているように、１枚１枚の極薄の側面積を積分して行けば体積になるのだ、と。個人的には前回よりもわかりやすいかも。コーヒー飲みながら積分するのがよろしいようで。
※「忘却の微分方程式」投稿順 index はこちら
※数学のお勉強のための以下の教科書（参考書、問題集？）の例題をMaximaの練習に使わせていただいております。
遥かなるかな太古の時代、大学生のときにこういう御本が欲しかったデス。
※以下のMaxima/wxMaximaバージョンで実習させていただいております。
-
- Maxima 5.46.0
- wxMaxima 22.04.0
今回の問題
以下のQ51をyとして表されるようなグラフとX＝０の線で囲まれた断面をY軸中心にグルリと回転させたときにできる体積を求める問題です。ただQ51みてもどんな形になるのだか想像もできません。
まずは、上記の「２次元の断面」のグラフを観察するとこんな感じ。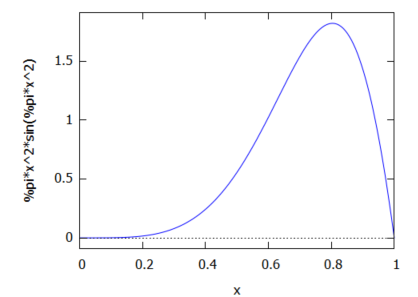
上のグラフを見てようやく体積のイメージをすることができるようになりました。実際に回転体の体積風に表現すると以下のようです。バームクーヘンというかドーナッツ型のケーキに見えなくもないです。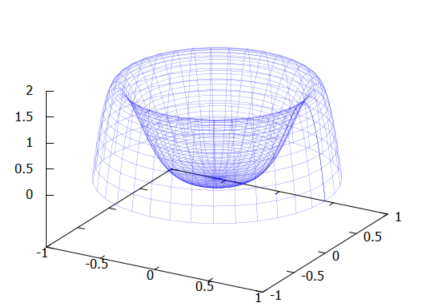
上記の３次元プロットを描くコマンドは以下のようです。回転軸をz軸に置き換えて、底面のx, y 平面上に動径Rが０～１の範囲を回っているイメージです。
なお、上記の３次元プロットを描くにあたって以下のページを参考にさせていただきました。あざーす。
バームクーヘン型求積法
この考え方はシンプルです。高さf(x)、周囲の長さ2πxがバームクーヘンの1層分の表面積（厚さは無限小）なので、これをx方向に必要なだけ積分していってやれば体積が求まると。こんな感じ。
上記にそって定積分を行ってみます。
問題を実際に解いたのはMaxima様ですが、答え1発。バームクーヘン型はおいしい？