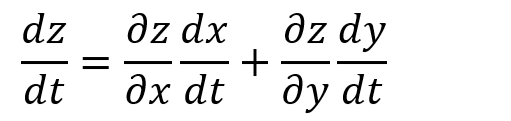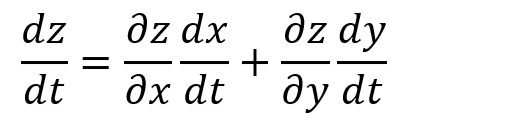前回は偏微分だろうが全微分だろうがdiff()関数におまかせの回だったです。今回は合成関数だろうが何だろうがやっぱりdiff()関数におまかせの回です。教科書的には定理を使って解いてね、という思し召しの回なのですが、定理使わんでも、無理やり定理に当てあはめてもMaxima様にお願いすれば結果は同じだと。
※「忘却の微分方程式」投稿順 index はこちら
※数学のお勉強のための以下の教科書(参考書、問題集?)の例題をMaximaの練習に使わせていただいております。
遥かなるかな太古の時代、大学生のときにこういう御本が欲しかったデス。
※以下のMaxima/wxMaximaバージョンで実習させていただいております。
-
- Maxima 5.46.0
- wxMaxima 22.04.0
今回適用すべき定理
zがx,y の関数で、x, yがtのみの関数、そのときzがx, yについて偏微分可能で、x,yがtについて微分可能、というのが今回のシチュエーション?っす
zの中のx,yをtで書き直すような無粋なことをしなくても解けるのよ、とうことであります。
今回の例題
今回の例題は以下のようです。上記の定理を適用せよという思し召し。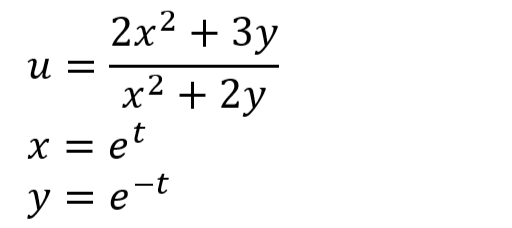
まずは、思いつくまま、素のまま以下のようにx, y そして uを入力してみました(Maximaでは自然対数の底は%eと書かねばならないのが微妙デス。)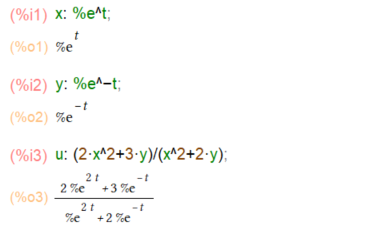
あれれれ、uを入力した時点で、x, y が代入されちゃってます。よって微分は以下のように一撃。tで微分するだけ。
微分した後の整理がちと面倒だったですがお答えには到達(教科書とは%eの係数の書き方がチト違うけれども。)
しかし上記では、定理を使えという思し召しには添えてないです(答えは出たけれども。)
解き方その2
tの関数であるx , y が即座に代入されないように、あえて別の変数名 X, Y ということでUを書き直し、それを使って定理を適用してみました。こんな感じ。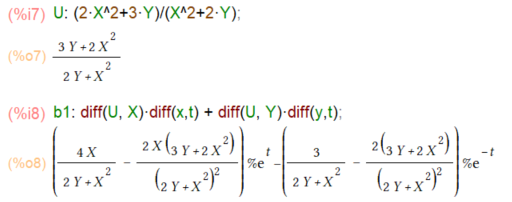
ちゃんと適用できてますな。しかし、X、Yと書いてある部分をtの関数で置き換えないと解答には到達できませぬ。そこでsubstしてみましたです。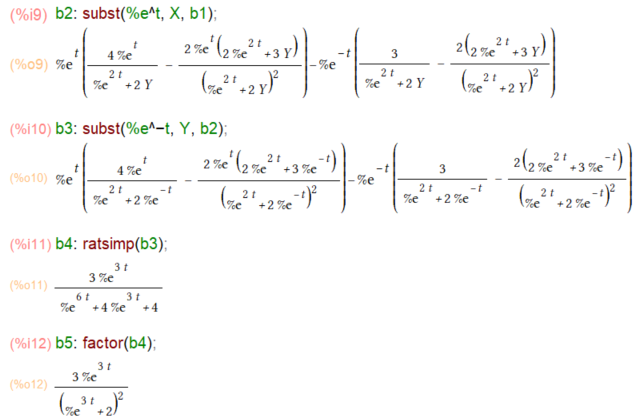
結局お答えは出ましたが、直接diff(u, t)するよりメンドくないかい、これ。
解き方その3
シングルクウォート(以下黄色のマーカ部)をつけることでMaxima様に勝手に式を評価しないようにお願いすることができます。それを使って uの代わりにuxyという名で書き直してみました。x, y は「そのまま」で定義できました。これを使って定理通りに微分をしてみました。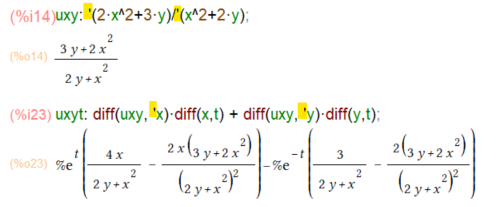
なお、diff(uxy, ‘x)みたいに微分する変数xのところにもシングルクウォートをつけてますが、これつけないとエラーで落ちます。つけなかった時点でxが評価されて%e^tに置き換わってしまうので、微分対象のuxyの中にそんな変数はないってことになるようです。
先ほどは上の形になったあと、無理やりsubstしてましたが、今回は多少エレガント?な処理で可能です。ev()使って評価が抑制されているx, y のところを評価してやれば処理をすすめることができます。こんな感じ。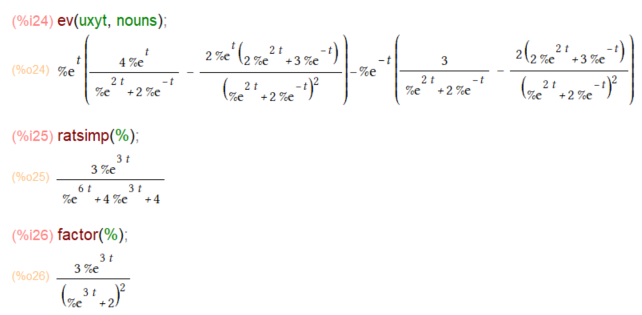
いろいろやってみたけれども、定理なんかお構いなしの最初の方法が一番単純明快、ステップも少ないじゃん。