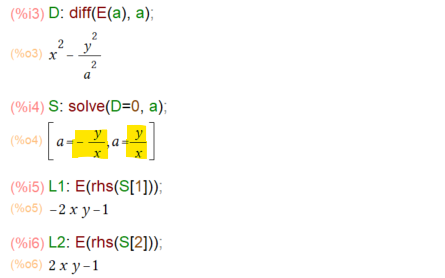最近SDR用のドングルを購入、個人的にひそかに無線づいてます。そのせいもあって「包絡線」などと聞くと耳がピクピクします（実際には動かないケド。）今回は曲線群 f(x, y, z)=0（aはパラメータ）の包絡線を求めよとの問題。まあ、求めよといって式だけでは寂しいので、Maxima様にお願いすればプロットまでほぼほぼ一撃。
※「忘却の微分方程式」投稿順 index はこちら
※数学のお勉強のための以下の教科書（参考書、問題集？）の例題をMaximaの練習に使わせていただいております。
遥かなるかな太古の時代、大学生のときにこういう御本が欲しかったデス。
※以下のMaxima/wxMaximaバージョンで実習させていただいております。
-
- Maxima 5.46.0
- wxMaxima 22.04.0
包絡線とその求め方
数学素人がくだくだ書くのは恐れ多いので、いつもお世話になっております「数学の景色」様の以下のページなどご覧くだされや。
ぶっちゃけ、計算手順的には曲線群の式をパラメータで偏微分してやるところくらいがメンドイ感じですが、Maxima様にお願いする場合は diff()一発です。
今回の問題
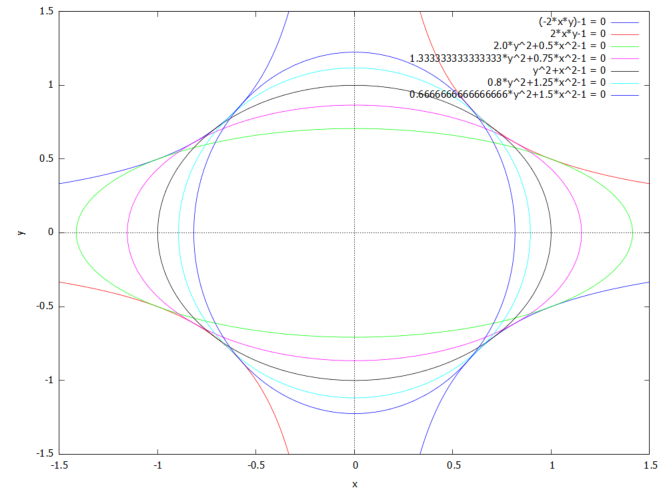
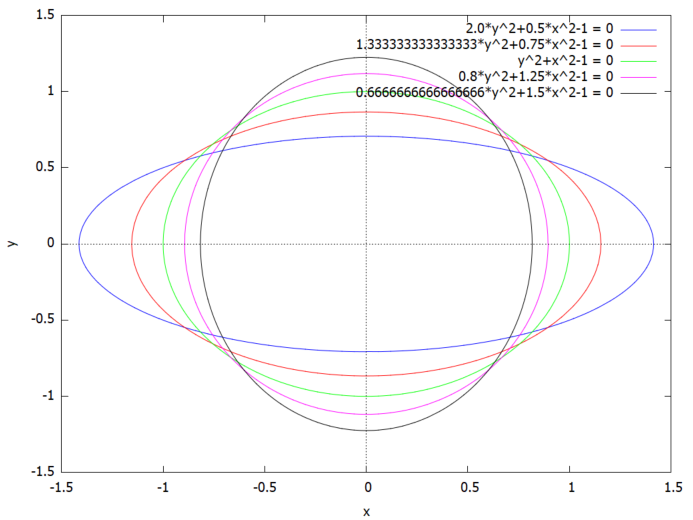
パラメータa でくくられる楕円の群れの包絡線を決定せよとの問題です。楕円は、E(a)=0。パラメータaのいくつかの値について楕円を描くのは以下のように。
実際に、楕円「群」を描いたものが以下に。
こうして楕円群をみているとそこはかとなく包絡線が見えるような気がしてくるのは気のせい？
包絡線を求める
包絡線をもとめるのは以下のような処理で可能っす。偏微分して、偏微分結果を=0とおいて解いて求めた解を、元の楕円群の式に代入すると。こんな感じ。
D: diff(E(a), a); S: solve(D=0, a); L1: E(rhs(S[1])); L2: E(rhs(S[2]));
実際に処理したものが以下に。
上記のL1、L2を＝０とおけば包絡線（陰関数）です。実際にさきほどの楕円群にL1、L2の包絡線を重ねたものが以下に。
包絡線ときくと「包絡線検波」が連想される今日この頃。