前回は包絡線(envelop)でした。今回は接平面です。「似たようなもん?」、偏微分して公式に当てはめればこの年寄にも式は求まります。でもね~実際に図を描いてみないと実感がわかないのよ。そして図を描くためには何か具体的な数値を与えないと描けません。具体的な数値にすれば納得いくけれどもメンドイ。しかたない?
※「忘却の微分方程式」投稿順 index はこちら
※数学のお勉強のための以下の教科書(参考書、問題集?)の例題をMaximaの練習に使わせていただいております。
遥かなるかな太古の時代、大学生のときにこういう御本が欲しかったデス。
※以下のMaxima/wxMaximaバージョンで実習させていただいております。
-
- Maxima 5.46.0
- wxMaxima 22.04.0
接平面
数学素人がぐたぐだ言ってもせんないので、接平面の公式は以下の通りです。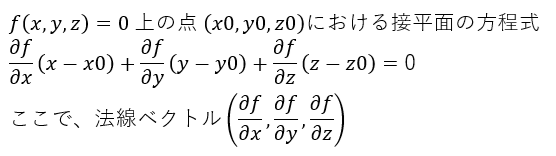
今回の例題
上記のf(x,y,z)にあたるものが、以下の楕円面を表す式です。
上記にあるように法線ベクトルを求めると以下のようになります。
しかし、後でプロットするときに具体的な座標を与えることになるので、接点を(x0, y0, z0)とおいて関数として定義しておくことにしました。この方が計算便利だし。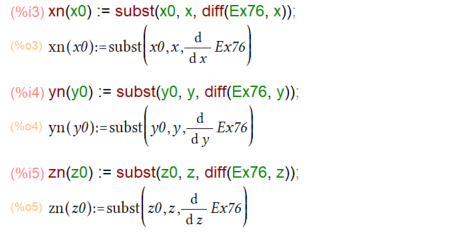
さてこれらを用いて接平面の方程式を決定することは一撃(上の方の公式に当てはめるだけだから)。こんな感じ。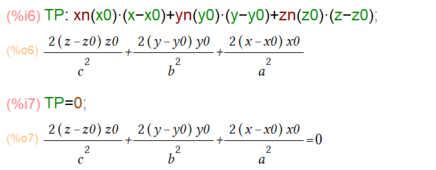
教科書的には上記のTP=0の式をチョイとテクを使って整理して、も少しシンプルな形にしてました。しかし、Maxima様にお願いするのであれば、式をシンプルにする必要など無(シンプルにするための処理の手数の方メンドイからやりたくないのだろ~が、自分。)
具体的なグラフを描く
上記で接平面の式は求まってしまったのですが、それを眺めていても実感がわきませぬ。とりあえずどこでもいいので接点を決めて接平面を描いてみることにいたしました。楕円面といいつつ、a=b=c=1 で球ということにし、接点はありがちな(1/√3, 1/√3, 1/√3)といたしました。x, y, zにゼロ以外の値が入っているのに暗算で求まる数少ない点でございます。具体数値の定義が以下に。
最後の行でホントに、(X0, Y0, Z0)が球面に載っていることを確かめております。
さて接平面の式TPに、具体的な数値を代入しております。やりかたよくわからなかったので、substしてしまいました。力業。
接点における具体的な式に書き直された接平面の式がTP0=0です。陰関数を3次元プロットする技を身に着けておりませんので、ことさらsolveかけて陽関数としております。まだa, b, cは混じってますが、具体数値を定義済なのでプロット可能な筈。
接平面を単独で描いてもなんだかな~なので、「接する」相手の楕円面(今回は球になる筈だけれども)を描く準備が以下に。やはり陰関数のままでは3次元プロットする方法が分からなかったので、solveして陽関数化してます。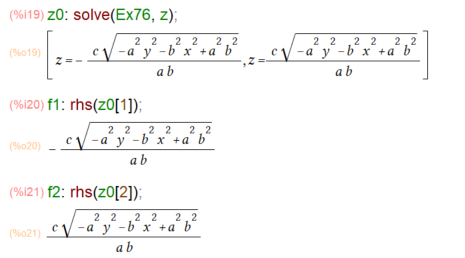
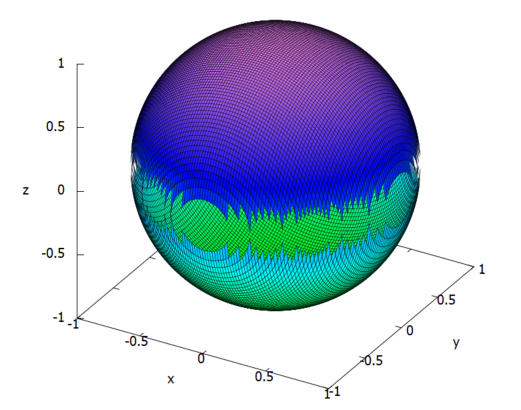
念のため、上記で求めたf1とf2をプロットしてみました。
plot3d([f1, f2, [x,-1,1],[y,-1,1]],[grid,100,100],[same_xyz, true]);
こんな感じ。
f1とf2のつなぎ目に結構断絶が大きくて(グリッドが粗い)、なにやらかのデススターのような絵ずらであります。
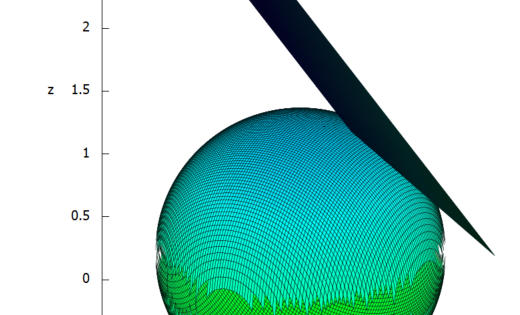
さて接平面もあわせてプロットしたものの一部が以下に(プロットが細長くて画面からはみだすので。)
plot3d([f1, f2, TP0, [x,-1,1],[y,-1,1]],[grid,100,100],[same_xyz, true]);
球面上の接平面のつもり。
描けたことは描けたが、いいのかこんな感じで。