
今回は前回の続きの二重積分です。前回よりも「微妙に」ムツカシくなっているのは、積分領域Dが「マルでも三角でもないちょっと複雑な形」になっているうえに、単なる数値じゃなく文字定数で記されているところです。文字のままではグラフが描けんな。とはいえ解くのはMaxima様なので、そんなことは知ったこっちゃね~。大丈夫か?
※「忘却の微分方程式」投稿順 index はこちら
※数学のお勉強のための以下の教科書(参考書、問題集?)の例題をMaximaの練習に使わせていただいております。
遥かなるかな太古の時代、大学生のときにこういう御本が欲しかったデス。
※以下のMaxima/wxMaximaバージョンで実習させていただいております。
-
- Maxima 5.46.0
- wxMaxima 22.04.0
今回の例題
今回の例題を清書したものが以下に。積分領域D1は根号ありの陰関数で表示されているうえに、その領域はa, bの文字定数で抑えられてます。メンドクセーです。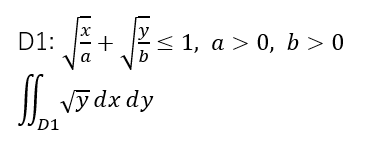
積分領域D1の図示
積分領域を図示せよとの教科書のご指示あり。D1を2次元のグラフに描くための準備をば、いたしまする。忘れずに assume から。
solveでxなりyなりで一撃で解けんかな、とも思ったのですが私メの拙い知識ではダメでした。正攻法で両辺2乗して解いてます。D1の領域的にはx=でもy=でも対称なのでどっちゃでも良いのですが、後で積分するときにxが先、yが後の方がすんなり解けたのでx=の形にしとります。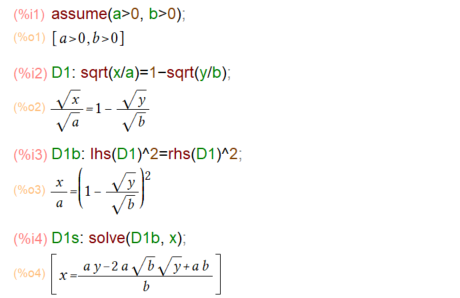
さて、領域D1の上側?を抑える式が求まったので、2次元グラフにしようと思いますが、残念ながらグラフにするためには、aとかbとか、文字で書かれた定数が邪魔です。私の拙劣な知識では具体的な数値にしないとMaxima様に描いていただけませぬ。そこで例によって力業、上記D1sの式に右辺を取り出してきて、substで具体数値を当てはめてしまいます。一番簡単なので、a=1、b=1ということでよろしく。こんな感じ。
描いたグラフは以下のとおり。縦軸をy、横軸をxにとった場合は、y=1のところは実はb、x=1のところは実はaなんであります。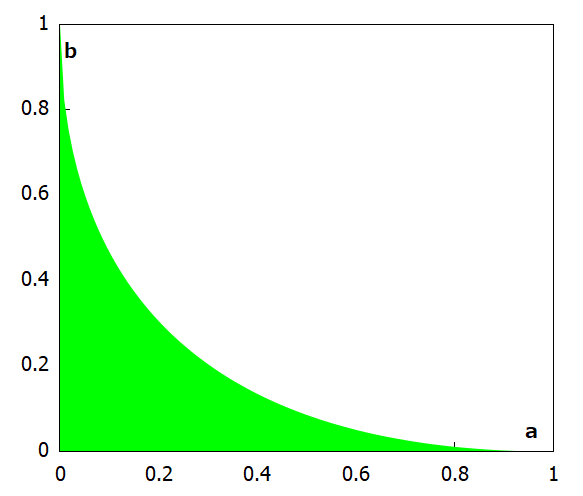
積分実行
まあ、上記の「準備」にて積分範囲が明らかになったので、それをそのまま式にし(例のようにシングルクウォートで、積分記号のままスンドメ。)、つづいてevで積分を実行してみたものが以下に。
お答えはバッチリみたい。ワタしゃ知らんけど。
