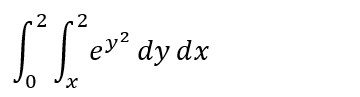今回、教科書的には二重積分の積分順序を変更すると御利益があるかも、の回です。順序変えたら計算がお楽になる、というのは人間にとってでしょうな。Maxima様にとってどうなのかはイマイチ分かりませんです。今回は教科書式の順序変更をやってお答えが出た後で、スイッチ一つつけたら変更せずに解けること発見。丸投げするのが一番？
※「忘却の微分方程式」投稿順 index はこちら
※数学のお勉強のための以下の教科書（参考書、問題集？）の例題をMaximaの練習に使わせていただいております。
遥かなるかな太古の時代、大学生のときにこういう御本が欲しかったデス。
※以下のMaxima/wxMaximaバージョンで実習させていただいております。
-
- Maxima 5.46.0
- wxMaxima 22.04.0
例題その１（積分順序変更せず）
以下、例題を清書したものです。
上記は、そのままMaxima様にお願いいたしましたるところ、特に順序を変えるような操作をせずとも解けてしまいました。
無理に順序変更する必要もなし。
例題その２（積分順序変更してみたケド）
このままだと、積分順序の変更の「練習」にならんな、ということで臨んだ例題その２が以下です。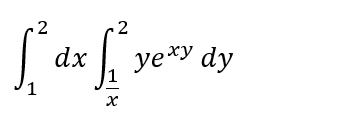
そのままで、Maxima様にお願いしたところ、お答えはでたものの、ちょっと予想外の形式です。
gamma_incomplete()って何？「第二種不完全ガンマ函数」だそうです。日本語マニュアルページへのリンクはこちら。
予想外の「第二種不完全ガンマ函数」登場にパニクリましたが、考えてみるに例題の積分範囲がチト不規則なのです。プロット操作が以下に。
draw2d(fill_color=green, filled_func=2, explicit(1/x, x, 1, 2));
プロット結果が以下に。
積分順序を交換するだけでなく、上記の積分範囲を「分割」して見通しをよくするのが人間的な定石かと。
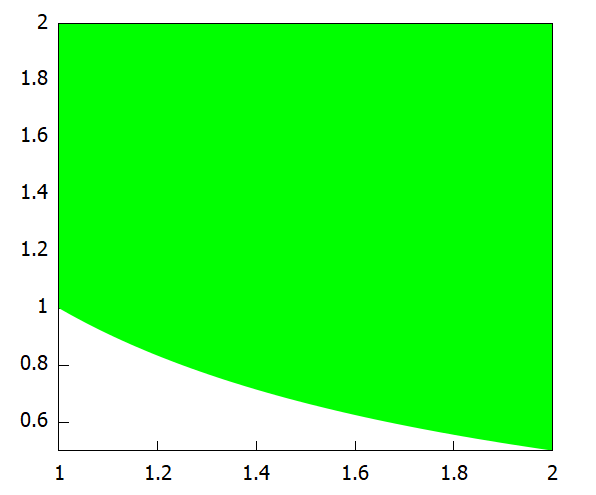
まずは下側の反比例で下限が決まっている部分。プロット操作的には以下です。
draw2d(fill_color=green, filled_func=1, explicit(1/x, x, 1, 2));
プロット結果が以下に。
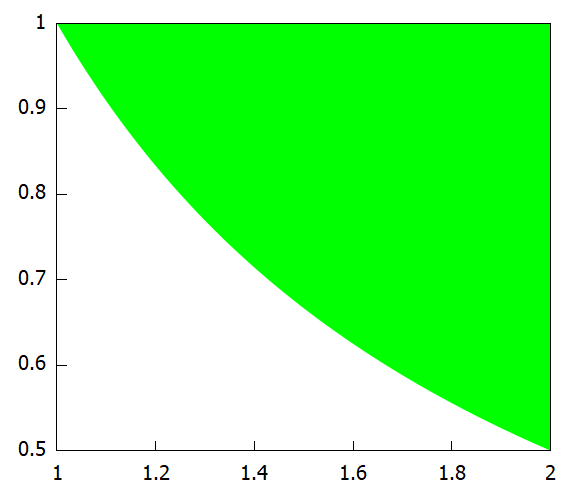
もう一つの上側の正方形部分。プロットコマンドは以下です。
draw2d(fill_color=green, filled_func=2, explicit(1, x, 1, 2));
プロットは以下です。
こうして積分領域がハッキリしたので、積分順序の変更も簡単にできるというもんでしょ。２つに分割したB領域とC領域を別々に積分して加え合わせてお答えにしたものが以下に。
お答えは求まったみたいっすけど、メンドイな。
「第二種不完全ガンマ函数」からでも解ける
しかしね、数あるMaxima様のオプションの中に gamma_expandという「ガンマ函数一族」の展開を左右するものがあることを見つけました。それを true に倒してみました。
なんだ、積分順序変更しなくても、領域分割しなくても一撃で答えがでるじゃん。