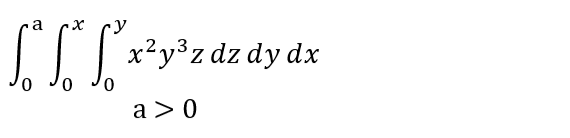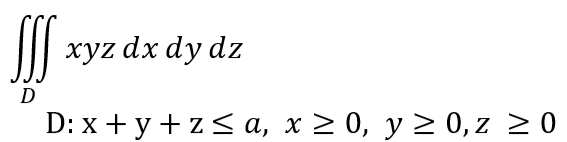長らく二重積分やってましたが、今回はフツーの三重積分です。まだまだ二重積分も三重積分も続くであろう教科書の流れです。今回は「箸休め」的な素直に三重積分の回かね。まあね、計算するのはMaxima様デス。Maxima様的には、二重だろうが、三重だろうがほぼほぼ関係ないっと。適切に積分領域を指定できさえすれば問題ない。何が？
※「忘却の微分方程式」投稿順 index はこちら
※数学のお勉強のための以下の教科書（参考書、問題集？）の例題をMaximaの練習に使わせていただいております。
遥かなるかな太古の時代、大学生のときにこういう御本が欲しかったデス。
※以下のMaxima/wxMaximaバージョンで実習させていただいております。
-
- Maxima 5.46.0
- wxMaxima 22.04.0
例題その１
例によって例題を「清書」したものをまず掲げます。以前は ’ で「評価をスンドメ」したMaxima様の出力で積分表現は十分と思っていたのですが、２重、３重となってやっぱり清書必要と思われたためです。
Maxima様への入力が以下に。例によって「まずassume」しておくのがよろしいかと。
assume(a > 0)
Ex83_1: 'integrate('integrate('integrate(x^2*y^3*z, z, 0, y),y, 0, x), x, 0, a)
ev(Ex83_1, nouns);
Maxima様の出力が以下に。答え一発です。
例題その２
例題「清書」が以下に。
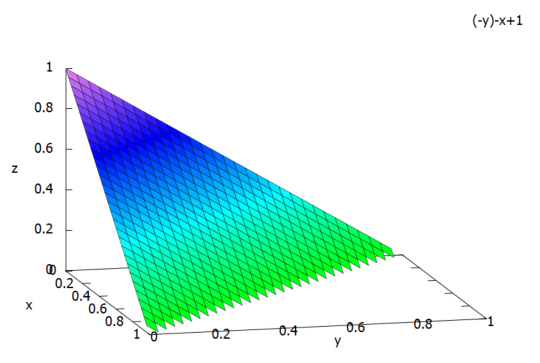
今回は積分領域がチョッチ複雑化してきたので、積分領域をグラフ化してみました。なお、定数 a のままではグラフに描けないので、a=1と具体的な値にしてます。
plot3d(1-x-y, [x,0,1], [y,0,1], [z, 0, 1]);
z=1-x-y のグラフが以下に。
上記の「斜面」とx=0, y=0, z=0の各垂直、水平面からなる「三角錐」が積分領域Ｄなんじゃぞ、ということらしいデス。
Maxima様への入力は、
Ex83_2: 'integrate('integrate('integrate(x*y*z, z, 0, a-x-y),y, 0, a-x), x, 0, a)
ev(Ex83_2, nouns);
上記に対するMaxima様のお答えはというと
積分領域Dの指定さえ間違わなければ、二重だろうと三重だろうと関係ないっと。ホントか？