物理やるときには線積分は避けて通れないです、知らんけど。メンドクセーと思いつつ、Maxima様にお願いするのであれば、定型どおりに機械的に計算すればお答えが求まる気がしてきました。ありがたいことだね。でもそんなんで大丈夫か？今回は２次元平面の中で線積分求める例題でしたが、３次元でもなんでも以下同文。ホントか？
※「忘却の微分方程式」投稿順 index はこちら
※数学のお勉強のための以下の教科書（参考書、問題集？）の例題をMaximaの練習に使わせていただいております。
遥かなるかな太古の時代、大学生のときにこういう御本が欲しかったデス。
※以下のMaxima/wxMaximaバージョンで実習させていただいております。
-
- Maxima 5.46.0
- wxMaxima 22.04.0
線積分(Curvilinear Integral)
例によって数学苦手の年寄が説明するのは憚られるので、「分かり易い」説明をネット上で探しました。いつもお世話になっております「高校数学の美しい物語」様の以下のページが分かり易いんでないかと。あざーす。
一方、教科書の例題を解くための「公式」的なところをまとめると以下のようです。このとーりに計算すれば線積分は求まるっと。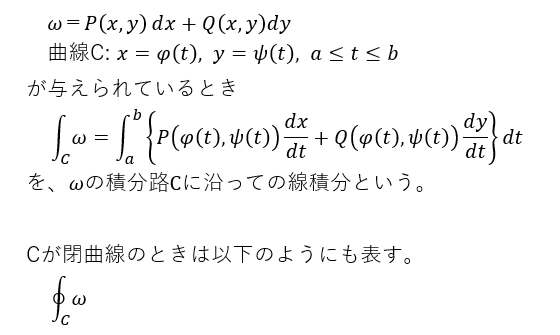
今回の例題
さて、具体的な例題は以下のようにまとめられます。
物理的にはなんたら「場」を表すのであろう関数P,Qは簡単。でも、経路は３通りも求めよと。経路をプロットしてみたのが以下です。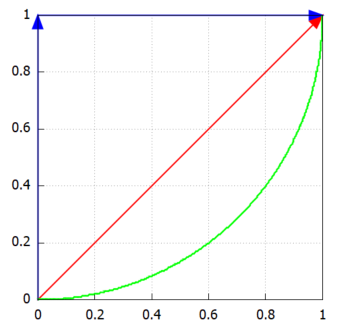
赤がC0、青がC1、緑がC2でやんす。なお、上記の三色プロットを描くためのコマンドが以下に。
s0: [0, 0];
e0: [1, 1];
m0: [0, 1];
draw2d(proportional_axes=xy, grid=on,
head_length = 0.05, head_angle=20,
line_width = 2, color = 1,
vector(s0, e0),
color = 2,
vector(s0, m0), vector(m0, e0-m0),
color = 3,
implicit(x^2+(y-1)^2-1, x, 0, 1, y, 0, 1)
);
赤線(C0)に沿っての線積分の結果
以下、線積分を計算するのにやっていることはC0、C1、C2とも形は同じです。上の方の公式通りに当てはめているだけ。最初は直行するC0経路。
波乱もなくお答えが求まりました。
青線(C1)に沿っての線積分の結果
つづいて、途中で折れ曲がるC1経路。最初に縦に上がるところを計算し、それから横に動くところを計算しているので、メンドクセーです。でもやることは一緒。まず縦。
続いて横に動いて、最後は合計。
まあ、計算できたみたい。
緑線(C2)に沿っての線積分の結果
最後は円を描く経路C2です。ついtでなくてθなどと書いてしまいましたが、やっていることは同じ。
同じことを４回も繰り返したので覚えたか？いや忘却力か？