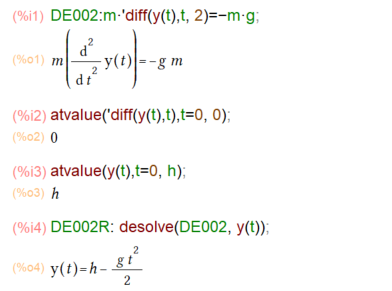教科書冒頭ということで、今回もアリガチな例題「重力による落下」の初期値問題であります。ソフトウエア業界の「HelloWorld」、電子工作業界の「Lチカ」にならぶ定番にして吉例なんであります。お答えは分かっているけれども、やらんわけにもいかないデス。御朱印帳にハンコを押す的な。微分方程式８８か所？そんなに練習するのか？
※「忘却の微分方程式」投稿順 index はこちら
※数学のお勉強のための以下の教科書の例題をMaximaの練習に使わせていただいております。ただし御本家『培風館』様のホームページで検索してみるも掲載されていないようです。絶版？ そのため以下のリンクは『Amazon』の通販ページであります。ご注意を。
※MaximaおよびそのGUIであるwxMaximaの以下バージョンを使用させていただいております。
-
- Maxima 5.46.0(x86_64-w64-mingw32)
- wxMaxima 22.04.0
今回の例題
わざわざ書くほどのこともないかと思いましたが、まずは「形」であります。こんな感じ。
という関数y(t)を求めて、グラフにしようと。
Maxima様に解いていただく
前回も復習いたしました手順は以下の通り。
-
- 微分方程式を「名詞形」で定義する
- atvalue()関数で初期値を与える
- desolve()関数で解く
実際のMaxima様への入力は以下の如し。
DE002:m*'diff(y(t),t, 2)=-m*g;
atvalue('diff(y(t),t),t=0, 0);
atvalue(y(t),t=0, h);
DE002R: desolve(DE002, y(t));
実行したところが以下に。
それではプロット
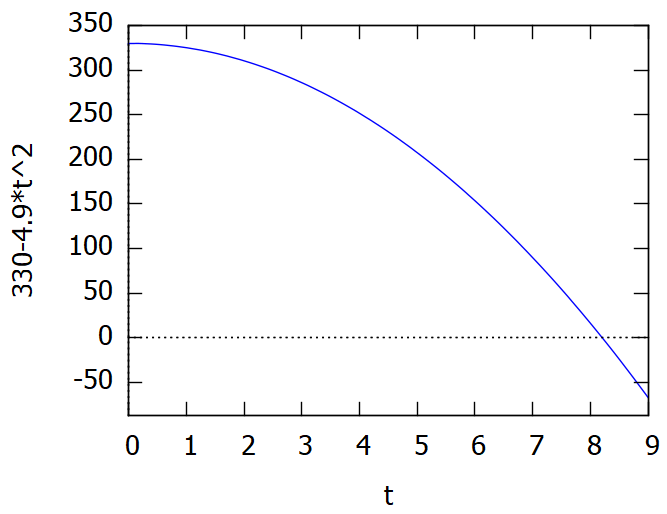
今回は「物理」からの例題ということでプロットを描かずにはいられませぬ。ただし、上記の解の定数部分（初期値）に何か数字を当てはめないとプロットできません。重力加速度は9.8 [m/s2]で決まり。高さhをどうするか。今回は、h=330[m]としてみました。東京タワーではないよん、麻布台ヒルズのつもり。流行に弱いんだ。定数の当てはめとプロット用コマンドが以下に。
プロット画面が以下です。
空気抵抗の無い真空中だと8秒チョイで地表に到達っと。