前回は吉例？「真空中の重力落下」でした。微分方程式の場合「吉例Lチカ」的な問題がいくつもあり、今回は放射性物質の崩壊（半減期）です。急速になのかダラダラなのか、ある一定の割合で崩壊していくアレです。Maxima様にお願いすれば微分方程式を解くのは一撃ですが、具体的な核種についてグラフを描かずにはいられませぬ。
※「忘却の微分方程式」投稿順 index はこちら
※数学のお勉強のための以下の教科書の例題をMaximaの練習に使わせていただいております。ただし御本家『培風館』様のホームページで検索してみるも掲載されていないようです。絶版？ そのため以下のリンクは『Amazon』の通販ページであります。ご注意を。
※MaximaおよびそのGUIであるwxMaximaの以下バージョンを使用させていただいております。
-
- Maxima 5.46.0(x86_64-w64-mingw32)
- wxMaxima 22.04.0
放射性物質の半減期と今回の例題
教科書の例題は比例定数kとか「数学風」だったので、変数名を物理風に書き変えた今回の例題は以下のようです。
微分方程式はシンプル。お答えは皆さんご存じのとおり、ある一定時間T（半減期）毎に残っている元の核種の原子数は半減していくと。
その辺お国も解説してますな。『環境省』様
まあ、放射性原子同士が談合しているわけでもなく、単にテンデンバラバラに崩壊していくのを「遠くから」眺めていると確率的にそう見える、というだけのことでしょうが。
微分方程式を解く
例によって微分方程式をMaxima様に渡せば、１，２の３で答えがでます。こんな感じ。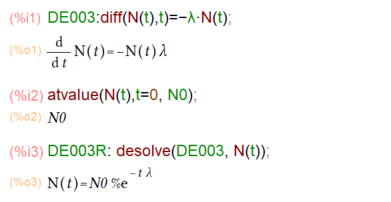
なお%eは、Maxima処理系の中での自然対数の底 e の表記です。
答えが出たので、何か特定の核種を当てはめてグラフを描きて～
崩壊定数λと半減期Ｔ
放射性物質の半減期Ｔは検索すればすぐにヒットしてきますが、崩壊定数λの方はメンドクセー数値になるせいか半減期Ｔから計算しろ、ってことみたいデス。Ｔからλを求める関数を定義しておきました。こんな感じ。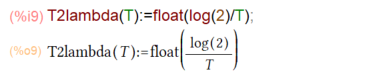
特定の核種の半減期Tから残っている原子の数のグラフを描く
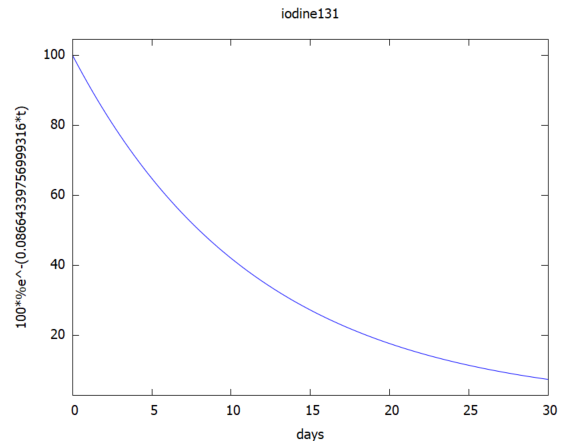
初期状態のN0=100（100個でも100％でも良い）として、半減期から残存原子をプロットしたグラフが以下に。
-
- ヨウ素131
半減期は８日ということで以下のようになる筈
プロットは以下に。
-
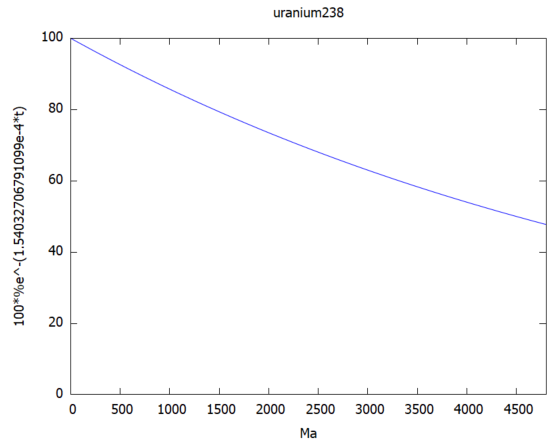
- ウラン238
半減期は約４５億年（地質学の単位Ma=100万年使うと4500Ma)ということで地球開闢以来のウラン238の残存量をプロットすると以下のようになるかと。
プロットは以下に
現代は、ウラン２３８がちょうど半分になったあたりなのね。ウラン235の方はとっくに少なくなっているケド。