安価に手に入る赤外線リモコン受信モジュールを使えば一撃なものを、わざわざ「生波形」から処理しようとしています。前回は包絡線検波(もどき)の自前関数を作製。でもそれ以前に変化する信号の2値化処理も行いたかったです。今回はそのための自前「もどき」関数を作製してみます。「もどき」ばかりで大丈夫か?
※「手習ひデジタル信号処理」投稿順 Indexはこちら
※Windows11上で、Scilab6.1.1およびScilab上のツールボックス Scilab Communication Toolbox 0.3.1(以下comm_tbx)を使用させていただいとります。
赤外線リモコンの「生波形」を取得した別シリーズ記事が以下です。
部品屋根性(112) AD8656でトランスインピーダンスアンプ、赤外線リモコン生波形
ターゲットの「生波形」
「生波形」と書いて、巷に跋扈する「生なんとか」をつい考えてしまう年寄です。「生ビール」は火入れをしていないビールということで「生」の根拠は大ありだけれど、「生」とそうでないのの違いが?なものもチラホラ。「生波形」はなんじゃらほい。知らんけど。
大分「急がば回れ」している気がしないでもないですが、以下の別シリーズでは、赤外線PINダイオードの出力を単電源、レールツーレールのCMOSオペアンプつかったトランスインピーダンス・アンプで電圧波形にすることで、赤外線リモコン受信モジュールを使ったらブラックボックスの中で見えない、38kHzのサブキャリアがアカラサマに見える「生波形」を取得しております。材料費考えたらもったいない使い方だあ。。。
しかし「生波形」を眺めていたら直ぐに気づくのが、
送信側を遠ざけたり、角度が変わったりすると振幅の変動が大きい
ということであります。生波形だからね、いろいろあるのよ。
そこで振幅の安定した信号にしておきたいと思いました。AGCという言葉もよぎりましたが、なんのアナログ波形じゃありません。ムツカシイ処理は不要っす。サブキャリアでもON/OFF波形、ほぼほぼデジタル。振幅の変化する波形からON/OFF、つまり1と0を取り出せればいいんじゃね。
ターゲット(テスト)波形の生成
自前の2値化(バイナリゼーション)関数を作製するまえに、例によってテストのための波形を生成しておくことにいたしました。リモコン波形に見立てるASK変調波形は以下の回で作成した genASK 自前関数で生成します。
手習ひデジタル信号処理(82) Scilab、ライブラリ再生成してみたけどダメ。自力更生。
上記で生成したASK波形の振幅がさらに変動する様子は、「遅い三角波」をASK波形に乗じてシミュレートしてみることにいたしました。そこで以下の回で作成済の
手習ひデジタル信号処理(59) Scilab、入力信号定義用の関数を手作り
genTriangular自前関数で三角波を作ろうとして「バグ」発覚。位相を0度から始めている分には0~1の値の三角波が出てくるのでOKなのですが、位相を変えると開始位置が変わりオフセットが載った値になってしまいます。ダメだ、これは。ということで修正したコードが以下に。
// Triangular wave (updated 2023/12/21)
// Fs: sampling frequency [Hz]
// nSample: number of samples
// fq: frequency [Hz]
// phdeg: phase [deg]
// mag: manitude
function [t,y]=genTriangular(Fs, nSample, fq, phdeg, mag)
dmag = mag / (Fs/fq/2);
t = ((1:nSample) - 1) / Fs;
tx = 2*%pi*(fq*t+(phdeg/360));
yd = dmag * squarewave(tx, 50);
tph = modulo(phdeg, 360);
if tph < 180 then
sum = mag * (tph/180);
else
sum = mag - ((tph-180)/180);
end
for i=1:nSample
y(i)=sum
sum= sum + yd(i)
end
endfunction
この修正後、以下のようにしてASK波形と三角波波形を乗じた波形をテスト波形といたしました。
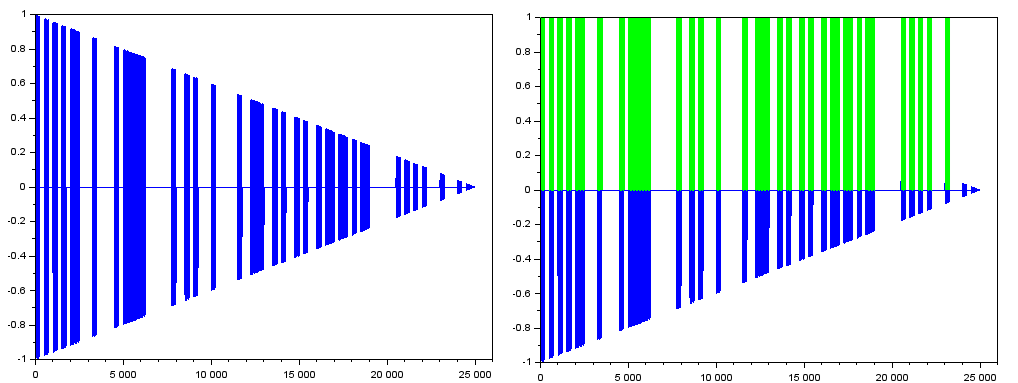
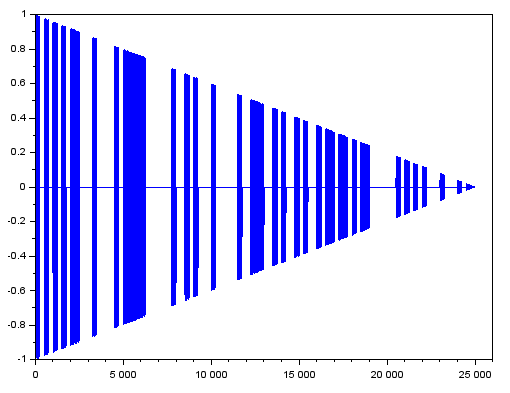
Fs=500e3; Fc=38e3; Fsym=2e3; Flev=10; m=1; b=prbs(100); askwave100=genASK(Fs, Fc, Fsym, m, b); [t0, TW0]=genTriangular(Fs, length(askwave100), Flev, 180, 1); twave = askwave100.*TW0'; clf; plot(twave);
2値化自前関数のソース
テキトーに移動平均値を作って、それ以上の値が信号に載っていれば1、載っていなければ0と判定する素朴な方法であります。ソースが以下に。
// binarization
// Fc: carrier frequency [Hz]
// Fsym: symbol rate [baud]
// Zcut: default level to zero
// w: input wave
function wo=makeBIN(Fc, Fsym, Zcut, w)
mav=ma(abs(w), Fs/Fc) - Zcut;
nSym=length(w);
for n=1:nSym
if w(n)>mav(n) then
wo(n)=1
else
wo(n)=0
end
end
endfunction
上記の関数をテスト用波形に適用してみる
ターゲット波形への適用とグラフ化の手順が以下に。
tm=makeBIN(Fc, Fsym, 0.1, twave); clf; plot(twave, "b"); plot(tm, "g");
遠くから眺めたグラフが以下に。黄緑が「バイナリ化」された波形、その下に隠れている青色が元波形です。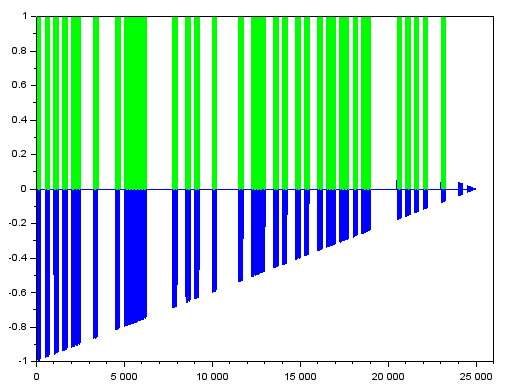
ほぼほぼ2値の波形になっているようだね。そんなんで良いのか。。。