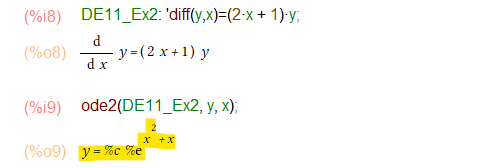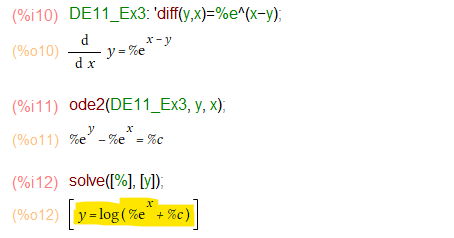前回まで、微分方程式を解くにあたってはdesolve関数にお願いしてきました。しかし、もう一つ解法があったのです。ODE2関数とな。ODE2のOはオーディナリのOみたいです。「常」微分方程式用ね。一階または二階の奴らを解くためのものみたいです。一般解を求めるときは、desolve関数でごちょごちょするよりずっとお楽。
※「忘却の微分方程式」投稿順 index はこちら
※数学のお勉強のための以下の教科書の例題をMaximaの練習に使わせていただいております。ただし御本家『培風館』様のホームページで検索してみるも掲載されていないようです。絶版? そのため以下のリンクは『Amazon』の通販ページであります。ご注意を。
※MaximaおよびそのGUIであるwxMaximaの以下バージョンを使用させていただいております。
-
- Maxima 5.46.0(x86_64-w64-mingw32)
- wxMaxima 22.04.0
ODE2関数
いつもお世話になっておりますMaxima様の日本語マニュアルの該当箇所が以下に。
ぶっちゃけ、今回の最初の例題を使って desolveで解くときと、ode2で解くときを比べてみたいと思います。左がdesolve、右がode2です。緑のマーカが微分方程式の表現。黄色がその解です。
上記例題は「y’=3*x^2」というごく簡単な微分方程式を求めよとのものです。desolve使う場合、yはxの関数なんだよね、ということをdesolve様に理解してもらわないとならないのでことさらにY(x)のような関数表現をしてます。また、任意定数Cみたいなものを勝手に紡ぎだしてくれないので、あくまで特殊解の「てい」でatvalue()関数で定数を与えたりしてます。
一方、ode2にお願する場合、ode2自体に従属変数名や独立変数名を与えないとならない分、上記のY(x)みたいなことさらな形は不要。そして、任意定数はよきに計らってくれて、%cなる「Maxima的にいかにも」な形で求めてくれます。
今回のような1階の常微分方程式、変数分離形で一般解を求める例題は ode2 の方が圧倒的に向いている?知らんけど。
例題2と例題3もやってみる。
例題2はちょいと複雑になりましたけど、ode2を使えば一撃であります(黄色マーカが一般解です。)お楽だ。
ode2で出てきたお答えは、対称で綺麗な形ではあるものの、教科書はy=の形のお答えを求めているので、最後の一ひねりが必要。といってsolve関数に渡して、y=の形に解いてもらうだけですが。末尾の黄色がお答えね。
いい感じで解けるじゃん、ode2。しかしな、ode2の「2」はどこから来てるの?もしかして2が付かないodeってのもあったの?