前回はASK変調を「深掘り」するとBPSK変調になる件?を計算。変調できるじゃんと思っていた無線素人の老人デス。しかし西村先生の御本を読んでいてホンマの無線ならサイドローブを抑えなければ使い物にならんだろ~とのご指摘。想定の赤外線通信ならありで押し通せる、とは思ったのですが、これもまた手習ひと。
※「手習ひデジタル信号処理」投稿順 Indexはこちら
※Windows11上で、Scilab6.1.1およびScilab上のツールボックス Scilab Communication Toolbox 0.3.1(以下comm_tbx)を使用させていただいとります。
※今回もお世話になったのは以下の御本です。
無線によるデータ変復調技術 西村芳一著 CQ出版 2002年
ただし、上記CQ出版社のページには悲しいお知らせあり『品切れ絶版』だそうな。アマゾンで古書買ってねってこと?
帯域制限
940nm波長の赤外線LEDを38kHzのサブキャリアで駆動するような想定の波形で手習ひしています。赤外線なら通常の無線のようにサイドローブで帯域幅が広いと混信して傍迷惑、といった話はありませぬ。電波法も関係ないし。しかしま、通常の無線であれば決められた帯域幅の中に押し込めないといけませぬ。そのためには変調前の信号を帯域制限かけてから変調するのが『スマート』とのお言葉であります。自前の変調関数共は、変調前の信号をノーフィルタでそのまま変調につかってます。マズイじゃん、これでは。変調関数、何度目かの作り直しね。
さてフィルタで帯域制限をかけるために、上記の御本ではいくつかのフィルタの例を挙げているのです。ますは最初の「ポンコツな」例としてRCフィルタ(抵抗1本、コンデンサ1個で作れるあれです)をあげてます。RCのローパス・フィルタでも帯域制限の効果はあるが、まったくもって不十分である、と。
Scilab上で、RCのローパス・フィルタを「エミュレート」して前回作成のサンプル信号に適用してみたら「ポンコツな感じ」が見えてええじゃないか、と考えました。やってみよう。しかし信号処理素人、RCのローパス・フィルタ、どうやってScilabでエミュレートしたら良いの?肝心なところが抜けてます。
なお、前回で使用したASK変調の信号波形(100%変調のとき)のノーフィルタの時のサイドローブの様子は以下のようです。
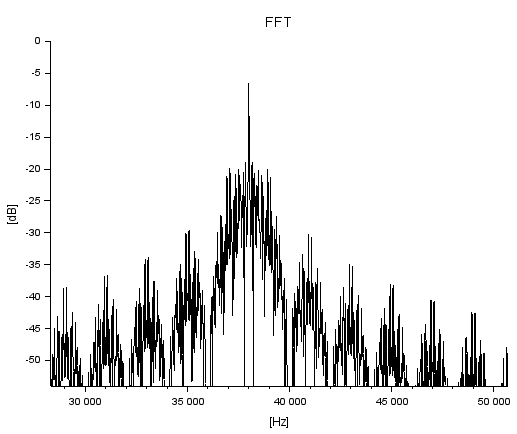
搬送波38kHz、シンボルレート2kHzです。38kHzを中心にして、プラスマイナスシンボルレートの整数倍で落ち込み、1/2シンボルレートのところではガッツリとしたサイドローブが観察できます。マズイじゃん。
Scilab上のフィルタ作成関数でRCローパス同等の特性を
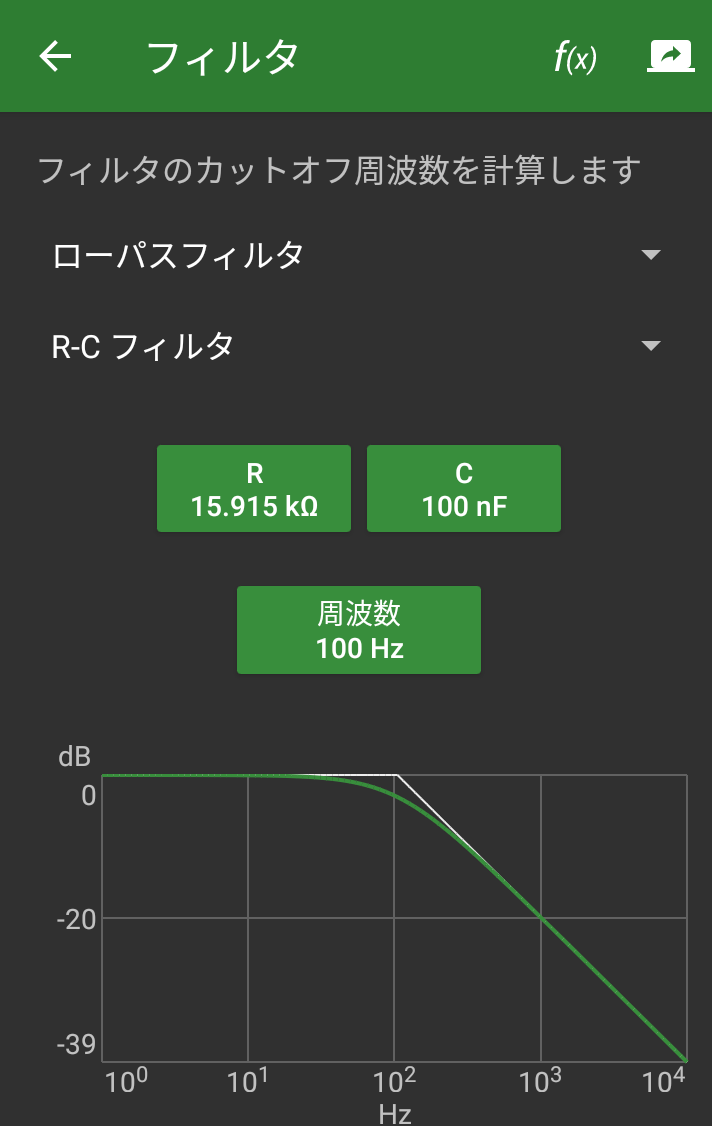
ハードウエアであれば、抵抗1本、コンデンサ1本持ってきて簡単に作れるRCローパスフィルタです。たとえばカットオフ周波数100Hzのフィルタを作るときはこんな感じ。以下はスマホに入れて愛用させていただいておりますアプリ Electrodoc ProのRCフィルタ設計ツール画面です。
忘却力の年寄は計算力もないので、このようなお道具なしには何の計算もできませぬ。上記のグラフを見れば分かるとおり、カットオフ周波数102Hz(100Hz)の10倍の周波数103Hz(1000Hz)にてゲインは-20dBであると。このRCフィルタの特性と「一致」するフィルタをScilab関数で設計して~という命題であります。
Scilabのアナログローパスフィルタ関数で計算
Scilabには analpf というそのものズバリの Analog Low Pass Filter 生成関数あり。ただしこれは、チェビシェフとか楕円とか実際に計算する者どもを選んで呼び出すためのドライバ関数みたいです。このうち、
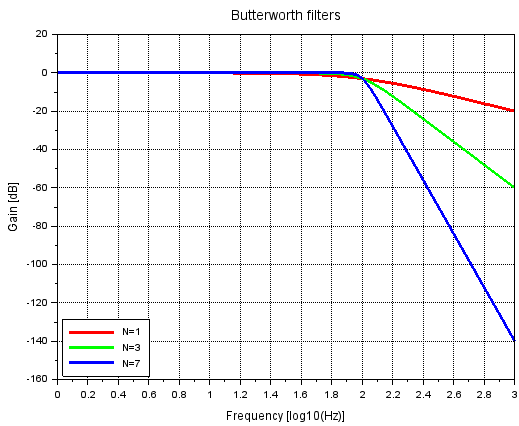
「1次のバタワースフィルタ」指定したらRCフィルタと一緒じゃね?
ということでやってみました。実験に使用したシーケンスは以下の通り。
fcut=100;
hb1=analpf(1,'butt',[0 0],fcut*2*%pi);
hb3=analpf(3,'butt',[0 0],fcut*2*%pi);
hb7=analpf(7,'butt',[0 0],fcut*2*%pi);
clf();
[fr, hf]=repfreq(hb1,1,1000);
plot(log10(fr),20*log10(abs(hf)),'r', 'LineWidth', 3)
[fr, hf]=repfreq(hb3,1,1000);
plot(log10(fr),20*log10(abs(hf)),'g', 'LineWidth', 3)
[fr, hf]=repfreq(hb7,1,1000);
plot(log10(fr),20*log10(abs(hf)),'b', 'LineWidth', 3)
legend(["N=1", "N=3", "N=7"], 3);
xgrid()
xlabel("Frequency [log10(Hz)]")
ylabel("Gain [dB]")
title("Butterworth filters")
赤の線が1次の特性です。100Hz(上のx軸の2)で-3dBを通過し、1000Hz(上のx軸の3)で-20dB付近を通過してます。これだね。この特性。
でもね、アナログフィルタの設計ができたとして、実際のサンプル信号(デジタルな数列)にどうやって適用するの?新たな問題が。これはまた次回。。。