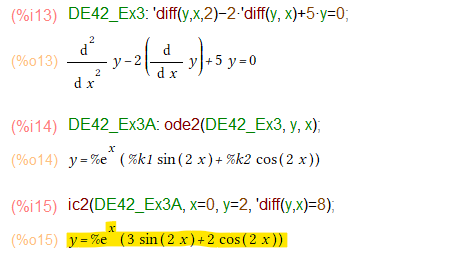ode2関数に1階微分方程式を食べさせたときに初期値問題を解くための関数 ic1を第129回で練習しました。今回、ode2に食べていただくのは「2階同次線形微分方程式」です。この場合に初期値問題を解くための関数は ic2 です。分かり易いっちゃ、分かり易い?でも bc2 というお仲間もいるみたいなんだけれども。
※「忘却の微分方程式」投稿順 index はこちら
※数学のお勉強のための以下の教科書の例題をMaximaの練習に使わせていただいております。ただし御本家『培風館』様のホームページで検索してみるも掲載されていないようです。絶版? そのため以下のリンクは『Amazon』の通販ページであります。ご注意を。
※MaximaおよびそのGUIであるwxMaximaの以下バージョンを使用させていただいております。
-
- Maxima 5.46.0(x86_64-w64-mingw32)
- wxMaxima 22.04.0
ic2 関数と bc2 関数
ode2関数は「一般解」を求めるための関数です。工学系分野なら多分一般解を求めてよし、ということはまずなくて、初期条件、境界条件を与えて解析することが普通でないかと。マニュアルページ(東北大様サイト)が以下に
-
- ic2関数、ode2関数で求めた一般解に対して、初期条件(独立変数のある1点における従属変数の値およびその時の1階微分の値)を与えて微分方程式を解く。多分、時間的な「発展」を見るにはこちらかと。
- bc2関数、ode2関数で求めた一般解に対して、境界条件(独立変数の2点における従属変数の値2つ)を与えて微分方程式を解く。多分、空間的な「分布」を見るにはこちらかと。
の2つの関数があります。ode2関数の御供、助さん格さんみたいなもの?
今回も教科書では手順を踏んで初期値問題を解く方法をお教えくださっているのですが、当方は、ode2の後に ic2を適用しているだけです。お楽。
例題1
ode2()関数によって、%k1、%k2を含んでいる一般解が得られたら、それをic2関数に渡し、さらにx=0でのyとy’の値を以下のように与えれば%k1、%k2の値が確定すると。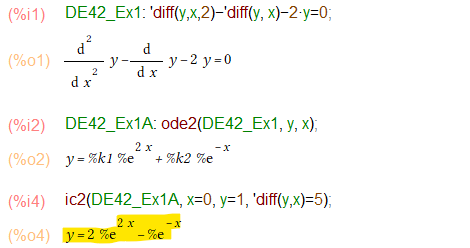
お楽に解けて良いなあ。
例題2
例題2の場合はic2の結果が教科書的にスッキリした形でなかったためにradcan(指数関数が出てくるので)に通してます。こんな感じ。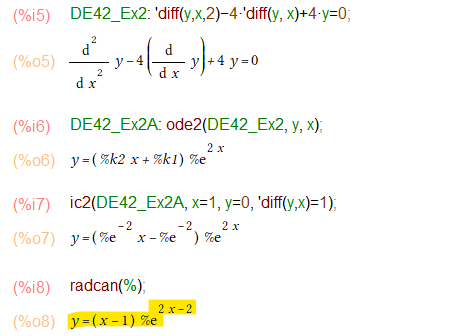
例題3
ic2使えば、初期値問題など一撃。それでいいのか?