前回まででScilabに存在するFIRフィルタ設計用の「代表的と思われる」関数４種を手習ひしてみました。FIRをやった（やっつけた）のであればIIRをやらないという分けにはいかんでしょうな。まずは設計関数を列挙。でもね、IIRフィルタの設計関数、過去回でやってみているのです。第１１６回ね。まずはそこのおさらいから。
※「手習ひデジタル信号処理」投稿順 Indexはこちら
※Windows11上で、Scilab6.1.1およびScilab上のツールボックス Scilab Communication Toolbox 0.3.1（以下comm_tbx)を使用させていただいとります。
ScilabのIIRフィルタ設計用関数
必ずしもこれだけということはないのですが、手元の環境のHELPを調べてみると、IIRフィルタを設計するのに使われそうな関数は、以下の４関数あたりではないかと思われました。
-
- eqiir
- syredi
- iir
- yulewalk
「１」のeqiir関数は、「２」のsyredi関数と本質的には同じアルゴリズムでIIRフィルタを設計するためのものみたいです。syrediのHELPを見ると計算アルゴリズムのFORTRANコード（1980年代にドイツで書かれたもの）へのリンクが示されてます。
https://michaelgellis.tripod.com/dsp/pgm25.html
歴史と伝統あるアルゴリズムなのね。ちょうど同時期、遥か半世紀前くらいにFORTRANを勉強した朧気な記憶があるものの、ソース読むのはパスしたいです。
「３」のiir関数は、アナログフィルタの連続な（sで書かれた）伝達関数を双一次変換(Bilinear Transform)を使って離散的な(zで書かれた）伝達関数に変換してIIRフィルタを得るものです。第116回で使ったのはこの関数でした。Scilabにはanalpfというアナログフィルタを計算できる関数（lpfというけれど、ハイパス、バンドパス、バンドストップみな生成可能）があるので、これ使えば一撃で変換できる？ホントか？双一次変換の変換式、sからzへは以下です。Tはサンプルリング時間間隔だと思います。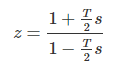
信号処理素人の老人はこの原理も分かっちゃいませんが、アナデバ様の石井聡先生が以下のページで説明されてます。分かり易い？私は、冒頭のヲタ話の方に気持ちが傾いておりますが。。。
TNJ-096: アナログ・フィルタの伝達関数をデジタル・フィルタに変換する「双一次変換」とは
「４」のyulewalk関数は「最小二乗フィルタを設計」と書かれてましたが、まだ調べてません。また使ってみるときに。
おさらい、HELPファイルの例をなぞってみる
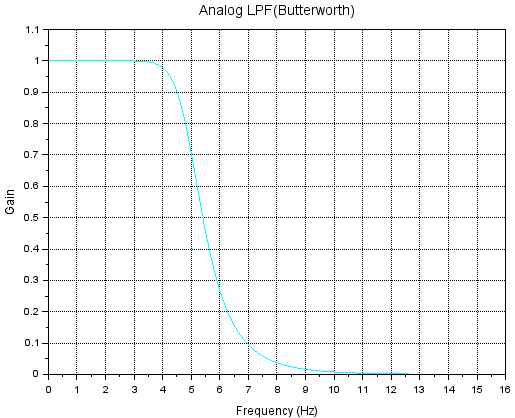
既に第116回で、iir()関数を使ってアナログフィルタと「ほぼほぼ等価な」IIRフィルタを作っているので、今回はHELPファイルの例にそっておさらいしてみることにします。まずは analpf()関数を使ったLPFの設計。
Fcut=5;
n=7;
hs=analpf(n,'butt',[0 0],Fcut*2*%pi);
hs.dt='c';
clf();
[fr, hf]=repfreq(hs,0,15);
plot(fr,abs(hf),'c');
xgrid();
xlabel("Frequency (Hz)");
ylabel("Gain");
title("Analog LPF(Butterworth)");
上記で生成したフィルタのゲイン特性が以下に。
肝心の伝達関数 Hsは以下のようです。
一方、IIRフィルタを使った場合の生成が以下に。上記のフィルタのカットオフ周波数が5Hzとなっていたので、とりあえずサンプリング周波数50Hzとしてみています。Fcutやnは上のまま。
Fs=50;
hz=iir(n, 'lp', 'butt', [Fcut/Fs, .25], [0 0]);
[hzm,fr]=frmag(hz,256);
clf();
plot2d(fr'*Fs,hzm')
xtitle('IIR LPF(Butterworth)');
xgrid();
xlabel("Frequency (Hz)");
ylabel("Gain");
q=poly(0,'q');
hzd=horner(hz,1/q)
上記から得られたゲイン特性が以下に。横軸は正規化周波数にサンプリング周波数を乗じてプロットしてます。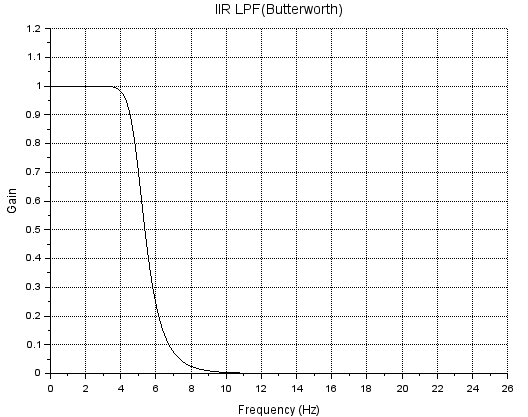
そして伝達関数が以下に、q=z-1のことです。
これが双一次変換で得られた式なのね（検算したわけじゃないけれど。）