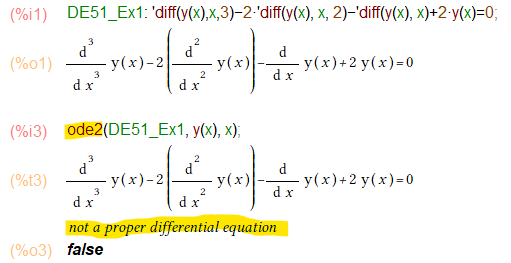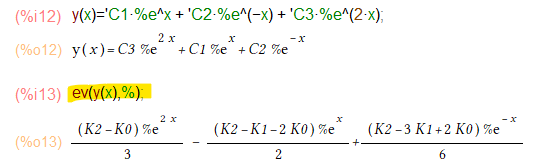このところずっと ode2関数の切れ味の鋭さに頼り切ってきました。しかし、とうとう限界です。今回は高階、といっても3階なのですが、2階を超えてしまいました。ode2のマニュアルページには1階、2階の微分方程式用だとハッキリ書いてあります。試みに3階の微分方程式を入力したらエラーになりました。どうする?
※「忘却の微分方程式」投稿順 index はこちら
※数学のお勉強のための以下の教科書の例題をMaximaの練習に使わせていただいております。ただし御本家『培風館』様のホームページで検索してみるも掲載されていないようです。絶版? そのため以下のリンクは『Amazon』の通販ページであります。ご注意を。
※MaximaおよびそのGUIであるwxMaximaの以下バージョンを使用させていただいております。
-
- Maxima 5.46.0(x86_64-w64-mingw32)
- wxMaxima 22.04.0
今回の例題
今回の例題が以下に
y”’-2y”-y’+2y = 0
とうとう3階の微分が登場してしまいました。これをいままで通りode2関数で解こうとすると以下のようになってしまいました。
not a properだと。。。ついに 伝家の宝刀 ode2()関数にも限界が来たのね。
desolve関数再び登場
一撃で、1階、2階の常微分方程式の一般解を求めてくれるode2()関数にどっぷりハマる以前は、desolve()関数に微分方程式をお任せしてました。desolve()は内部ではラプラス変換使って微分方程式を解く関数みたいです。どちらかといえば初期値を与えて特殊解を求めるときに向いてます(個人の感想っす。)一般解を求めるためにはあらかじめ atvalue()関数で、初期値として適当な文字定数を割り当てておくのが良いみたいっす。以下はテキトーにK0、K1、K2をatvalueしてます。
desolveすれば上の黄色のマーカのように微分方程式が解けました。しかし、K0、K1、K2とか定数で書いても煩雑な感じがするのは否めません。
なお、事前にatvalue()関数で初期値に文字定数を与えておかないでもdesolveによって解くことは可能です。しかし結果は以下のようにもっと煩雑。
上記では、y(x)の2階微分のx=0のときの値など、初期条件がモロに解の中に登場してます。なお、上記で「縦棒表現」に使われているのはat関数です。例えばy(x)の2階微分のx=0のときの値などは以下のようにして表現されとります。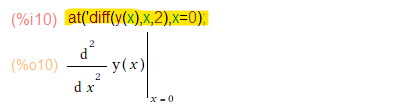
そこでK0、K1、K2などの事前定義の定数を以下のようにさらにまとめてしまうようにいたします。これは、ほぼほぼ手作業だけれども。
最後に出てきた黄色のマーカの形が教科書的にOKな感じの一般解でないかと。ここまで遠い道のりだったな。なお、以下のようにすれば元のK2/1/0つかった表現(あるいはat関数使った表現)に戻すことは簡単。
desolve使えば三階の微分方程式でもとけるっちゃ解けるけれども、一般解をキレイな形にするのはメンドイっす。