前回、前々回と練習してきたIIRフィルタ設計関数ですが、今回はその３回目。練習するのはyulewalk()関数です。「最小二乗フィルタを設計」とHELPページのタイトルに掲げられてますが、それをするのに使っているのがYule-Walker方程式みたいです。またメンドクさそうな奴を関数名に頂いておる設計関数だよ。
※「手習ひデジタル信号処理」投稿順 Indexはこちら
※Windows11上で、Scilab6.1.1およびScilab上のツールボックス Scilab Communication Toolbox 0.3.1（以下comm_tbx)を使用させていただいとります。
IIRフィルタの設計関数、yulewalk()
お名前の件をほじくっていくと、Yule-Walker方程式に引き込まれること必定なので、数学不得意の年寄は飛びのきます。まあ、計算アルゴリズムに踏み込まなくても使うことはできると。いいのかそれで。今回関数のHELPページが以下に。
計算アルゴリズムを棚にあげてしまって引数の与え方だけをみると、第１１９回で練習したFIRフィルタ設計関数の fsfirlin にちょっと似てます。所望のフィルタ特性の「グラフ」を関数に与えるとそれに近いフィルタを設計してくれるっと。分かりやすいっちゃ、分かり易い。
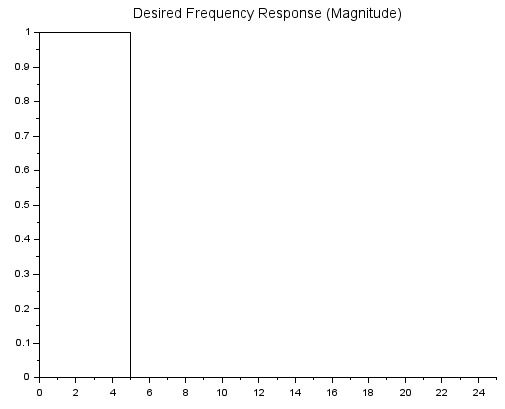
目標の与えかたは周波数ベクトル（正規化周波数）と、それぞれの周波数ポイントでの振幅をベクトルで与えるだけ。サンプリング周波数50Hz、カットオフ周波数10Hzのローパスフィルタを目標にする場合はこんな感じ。
Fs=50; Fc=10; f=[0,Fc/Fs,Fc/Fs,1]; H=[1, 1, 0,0];
なお、fは０から始まって1（サンプリング周波数）までとするべきなようです。上記でLPFのカットオフのところは垂直な壁になってますが、そういう与え方でも良いみたい。まあ、目標は目標、実際はそうなるわけではないけれど。
上記のfとHで表される所望の周波数応答の形を表示するコードが以下に。
fhz = f*Fs/2;
clf;
plot2d(fhz', H');
xtitle('Desired Frequency Response (Magnitude)')
結果のグラフは以下です。
IIRフィルタを生成
フィルタを設計してもらうのは簡単、コードが以下に。
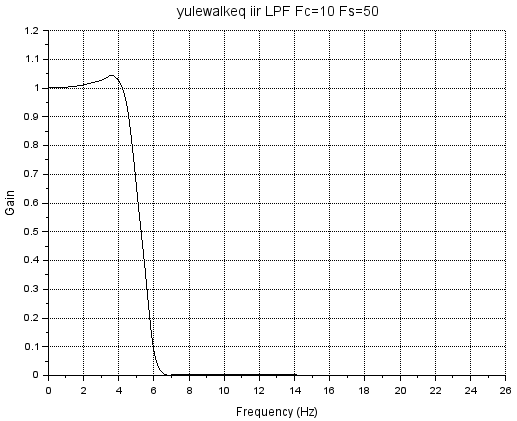
N=10; Hz=yulewalk(N, f, H)
上記で生成された伝達関数Hzが以下に。
これの周波数応答を求めてみると
[hzm,fr]=frmag(Hz,256);
clf();
plot2d(fr'*Fs, hzm');
xtitle('yulewalkeq iir LPF Fc=10 Fs=50');
xgrid();
xlabel("Frequency (Hz)");
ylabel("Gain");
グラフが以下に。
周波数5Hz付近でGainが0.7を通過しているので、カットオフは5Hzってか。まあ計算アルゴリズムは分かってなくても、計算はできると。。。