「サイエンティフィックPythonのための」IDE、Spyder上にてScientific Python Lecturesの実習中。前回は「線形代数」、今回は「補間」です。補間する対象の数列は、前々回の「特殊関数」の中から選択。トビトビの値を補間してグラフを描いた上に、数値的に微分までしてしまおうと。意外と盛沢山?
※「 ソフトな忘却力」投稿順 Index はこちら
※Scientific Python Lectures様のコースは例題だけでなく、エクササイズなども充実、それを全部順番に解いていったら必ずや立派な人になれるだろ~とは思います。でも量が多過ぎて死ぬまでに終わらない老い先短い年寄なので、適当に勝手に練習してお茶を濁してます。今回は、「5.4 Interpolation: scipy.interpolate」です。
レクチャでの補間の題材関数
測定データでもあれば「補間」する材料には事欠きませんが、サンプルプログラムです。レクチャでは
-
- 三角関数つかって何点か求めておいて
- そこに誤差乗せた点を用意、それを補間してグラフを描く
- 元の三角関数の計算点から途中を補間してグラフを描く
- 元の三角関数の計算点から途中を補間して微分(積分)を求めてグラフを描く
といった塩梅で、補間を味わってます。そこで三角関数使ってしまうと、レクチャともろ被りデス。芸がありません。そこで「似たような形の周期関数」を前々回の特殊関数の中から選ぶことにいたしました。でも誤差とか載せるのメンドいので、2はパスして、素の関数のまま。
楕円関数
そこで登場願ったのが、「複素関数」という恐ろし気なオーラをまとった楕円関数です。楕円関数といっても色々あら~ね、ということで、今回のものはヤコビの楕円関数と言われているものです。数学素人老人がごたくを並べても仕方ないので、前々回もお世話になっております「特殊関数グラフィクスライブラリー」様の以下のページなどを御参照くだされ。
https://math-functions-1.watson.jp/sub1_spec_090.html
上記ページには、楕円関数(そして楕円積分)の解説とともに、複素平面上の美麗なグラフ多数。ただ、数学不得意な老人は、実数範囲で実数の結果が得られるような部分で、SINに「似た」挙動を示す関数のみを切り出して使わせていただいとります。ヘタレ。
なお、SciPyの楕円関数関係のAPIマニュアルは以下に。
https://docs.scipy.org/doc/scipy/reference/generated/scipy.special.ellipj.html
補間
SciPyの補間に関するチュートリアルページが以下に。
https://docs.scipy.org/doc/scipy/tutorial/interpolate.html
素人老人は、補間というと2点を直線でつないで「案分」するような単純なやつしか使いませぬが、SciPyなどを使う場合は、キュービックなスプライン補間が人気のようです。
Googleの生成AI、Gemini 2.5 Flash様に解説いただいたスプライン補間についての説明が以下に。
この後、Gemini様は、3次のスプライン補間で課される条件や、スプライン補間の得失について論じられているのですが、そこは省略。すみません。
SciPy使ったサンプルプロット
以下はSpyder上で作成した、サンプルプログラムです。
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
"""
Created on Thr Jun 15 2025
@author: jhalfmoon
Jacobi's elliptic function and interporation plot sample
"""
import numpy as np
import matplotlib.pyplot as plt
import scipy as sp
def main(m):
t = np.linspace(0, 10, 25)
j = sp.special.ellipj(t, m)
ipT = np.linspace(0, 10, 200)
interp_spline = sp.interpolate.make_interp_spline(t, j[0])
interp_results = interp_spline(ipT)
d_interp_spline = interp_spline.derivative()
d_interp_results = d_interp_spline(ipT)
plt.scatter(t, j[0], s=2.0, color="blue", label="Elliptic")
plt.plot(ipT, interp_results, linestyle="dashed", color="green", label="Spline")
plt.plot(ipT, d_interp_results, linestyle="dotted", color="red", label="Derivative")
#plt.scatter(t, j[1], s=2.0, color="red")
plt.xlim(0, 10)
plt.ylim(-1.5, 1.5)
ax = plt.gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.spines['bottom'].set_position(('data',0))
ax.yaxis.set_ticks_position('left')
ax.spines['left'].set_position(('data',0))
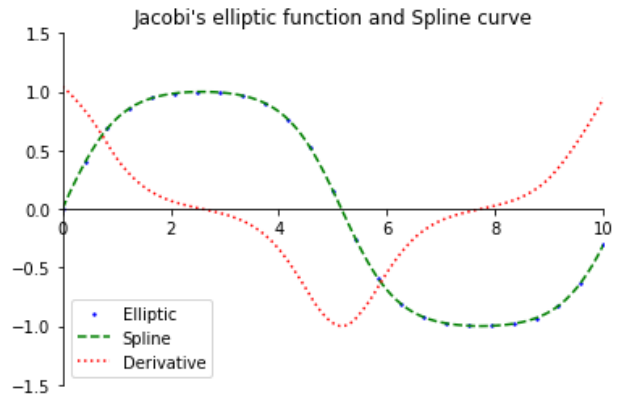
plt.title("Jacobi's elliptic function and Spline curve")
plt.legend(loc='lower left')
plt.show()
if __name__ == '__main__':
main(0.9)
関数ellipjは、2つの引数をとり、その第1が上記では t、第2をmとしています。結果は4つの配列のタプルとして返ってきます。上記で取り出している j[0] はsn(t, m)に相当(サイン関数に似ているもの)、j[1]はcn(t, m)、j[2]はdn(t, m)みたいです。j[3]はなんなんだろ~。すみません、調べてません。
mの範囲は 0≦m≦1 に制限されてます。main()関数を呼び出すときに mの具体数値 を与えることで、SINに似ているけどちょっと違う波形の雰囲気をいろいろ味わうことができます。なお、特殊関数グラフィクスライブラリー」様の楕円関数ページに、上記の 0≦m≦1 制限があっても、実数 m>1 の結果を計算するための変換方法が書かれてます。
プロット結果
緑色の小さい点が、実際にellipj関数を呼び出して値を求めた点です。0から10の間で僅かに25点です。それに対して、緑色の破線はスプライン補間を行った結果です。そして赤の点線は、余勢を駆って緑の線を数値微分してしまったもの。勿論、積分もできるみたい(やってないケド。)