「サイエンティフィックPythonのための」IDE、Spyder上にてScientific Python Lecturesの実習中。前回は関数の根、ニュートン法は不滅。今回はレクチャと異なり線形計画法です。老人のアップデートされていない頭ではシンプレックス法という名が鳴り響きますが、最近はモダンな方法があるみたい。
※「 ソフトな忘却力」投稿順 Index はこちら
※Scientific Python Lectures様のコースは例題だけでなく、エクササイズなども充実、それを全部順番に解いていったら必ずや立派な人になれるだろ~と思います。でも老い先短い年寄には量が多過ぎて多分死ぬまでに終わりません。適当な練習でお茶を濁してます。しかし、今回は前回につづき、「5.5 Optimization and fit: scipy.optimize」配下の「5.5.1 Root Finding」の「つづき」です。
レクチャの章立てでは「5.5.1 Root Finding」で関数の根を求めた後、「5.5.2 Curve fitting」に入ることになっとります。しかし、前回、SciPyのRoot FindingのAPIを眺めていて気付いてしまいました。Root findingの下の方に
Linear programming(線形計画法)
があることを。老人のアップデートされていない頭の中では、線形計画法というと「シンプレックス法」という御名前が半世紀くらい前から鳴り響いております。アップデートされていない頭で50年くらい暮らせていたわけだから、幸せな暮らしと言えましょう。
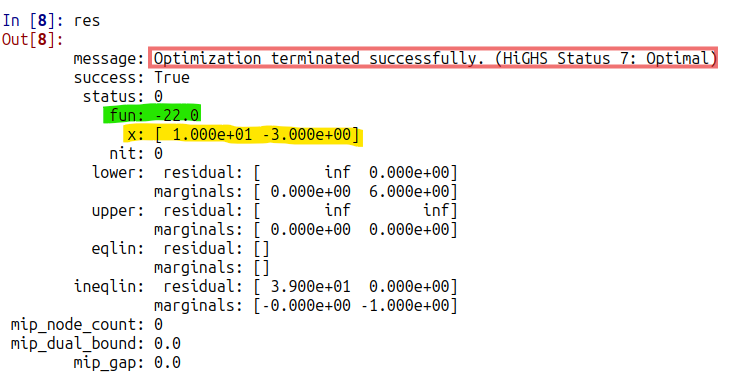
しかし「シンプレックス法」の発明?発見?は第二次世界大戦直後らしいです。流石に80年近くも「素のシンプレックス法」一本槍というわけでないよね。そしてSciPyのAPI解説ページには以下の警告が(赤枠はお惚け老人が書き加えたもの。)
そっか、simplex法は流石に 第一線を退いて、highsというアルゴリズムがSciPyでのデフォルト算法になっているのね。
例によって、Googleの生成AI、Gemini 2.5Flashに教えていただきました。まずはシンプレックス法について。
なんだ、シンプレックス法とまったく無縁な方法、というわけでもないみたいね。お任せすれば良きに計らってくれるみたい。お楽。
線形計画法の例題
以下のページの下の方に線形計画法のExamplesがありました。
説明されている linprog 関数は上位層のラッパ関数みたいで、オプションによっていろいろなアルゴリズムが呼び出せるみたい。Examplesでは特にアルゴリズムの指定が無いので今や simplex法に「とってかわった」HiGHS法?で解かれる筈。
このExampleでは
-
- 決定変数は x (1次元の2要素ベクトル)
- 目的関数は c @ x。これを最小にする、というのが目的。 なお、cも1次元の2要素ベクトル
制約条件は以下のとおりだけ。
-
- A @ x <= b、Aは2x2行列、bは1次元2要素のベクトル
- ベクトルxの第1要素x0については上限、下限の縛りなし。
- ベクトルxの第2要素x1については下限縛りのみあり、-3。
これをExample通りに解くシーケンス(ほぼコピペ)が以下に。
ちゃんとHiGHSで成功裏に解かれているみたい。いちおう目的関数 c @ x を計算したところが以下に。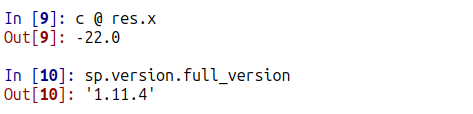
なお、SciPyのバージョンは上記のごとし。