信号処理素人老人がScilabの「信号処理のデモ」を物色中だった筈が、いつの間にかカテゴリ脱出。今回は「シミュレーション」カテゴリの中の「常微分方程式」の中の「ベクトル場」シミュレーションを一気に３つ鑑賞させていただきます。個体群動態にリミットサイクル（極限周期軌道）も登場。これって相平面解析ってやつ？知らんけど。
※「手習ひデジタル信号処理」投稿順 Indexはこちら
※Windows11上の Scilab2024.0.0を使用させていただいております。（Scilabについては御本家 Scilab 様へ）
１次元のベクトル場
最初に登場するのは、まずはお楽なところからということなのか、「１次元のベクトル場」です。以下のデモの選択画面から行います。クリックするとメッセージボックスが現れ、使用方法を説明してくれます。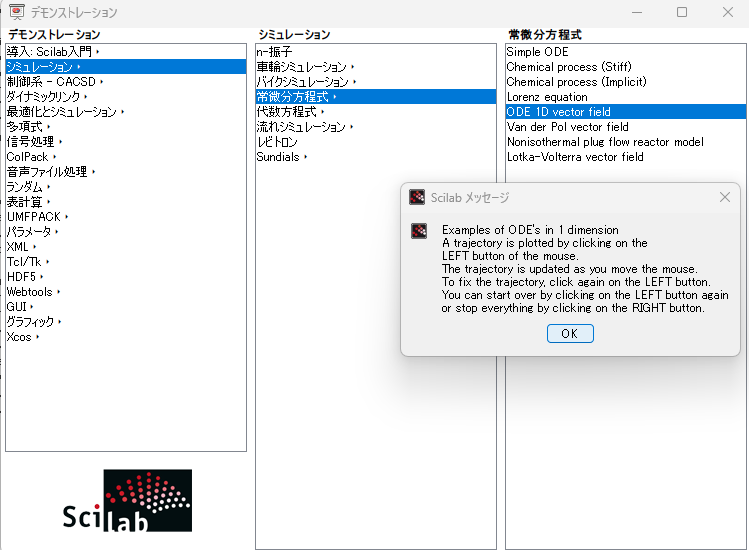
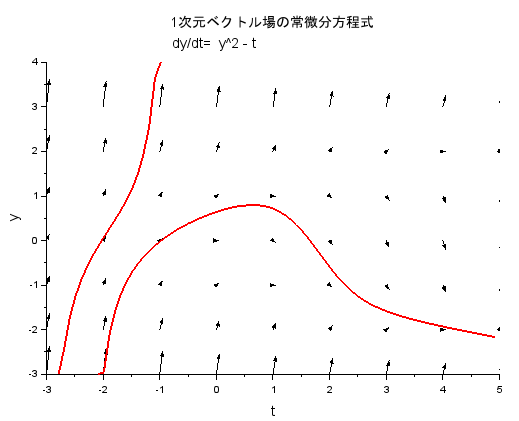
システムは、時間 t と位置 y の関数として常微分方程式記述されている「ベクトル場」です。１次元なので、見栄えよくプロットできるのか？というと、時間 t をもってきて、時間につれて「発展」していく様子を２次元プロットするみたいです。そこで使用される Scilab の関数が
champ
です。位置 (x, y) におけるベクトル(fx, fy)を矢印でプロットしてくれる関数です。今回は時間 t を x に当てはめています。
プロット結果が以下に。
上記の赤線は、「使い方」のメッセージボックスにあるとおり、矢印プロットでベクトル場を表示した後、適当な点でマウスの左クリックをすることで描かれる軌道です。なお、上記のデモのソースファイルはデモ・フォルダの配下に格納されている以下です。
ode_1dvect.dem.sce
ヴァン・デル・ポール方程式
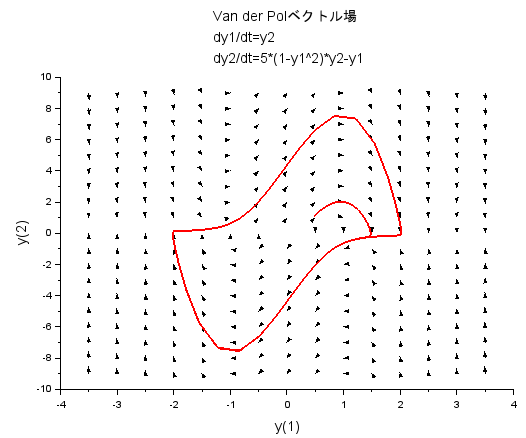
ヴァン・デル・ポール方程式によるベクトル場を描くデモは以下から選択できます。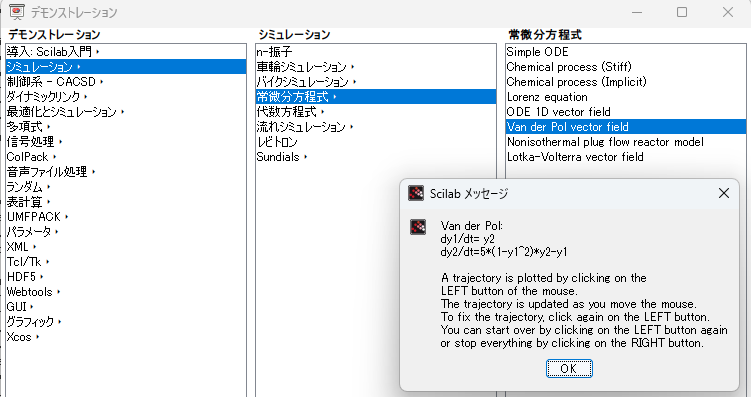
該当のソースファイルは以下です。
ode_vanderpol.dem.sce
ここで登場するヴァン・デル・ポール方程式は、「知らないとモグリ」的な方程式らしいですが、お惚け老人はもとよりモグリです。ここはGoogleの生成AI、Gemini 2.5 Flash様に解説をお願いしています。
おっと、シミュレーションで使っている方程式の形とはちょっと違うよ、大丈夫か？しかし、Gemini様は全てお見通しデス。
シミュレーションで計算しているのは、上記の「状態空間表現」でした。そしてこちらこそ、相平面解析で使われる形だと。やったね。
それに真空管の発振だけでなく、「自己組織化」とかモダーンな分野でも登場してくるのね。
そしてリミットサイクル（極限周期軌道）についても解説してくれています。
以上を踏まえて以下のプロットを御覧じろ。
私は、ちょろっと真ん中辺を左クリックしただけなのですが、そこから出発した軌道は、直ぐに大きな「周回軌道」に引き込まれてしまいました。他の点から初めても同じデス。リミットサイクルの威力？
ロットカ＝ヴォルテラ方程式
ロットカ＝ヴォルテラ方程式によるベクトル場を描くデモは以下から選択できます。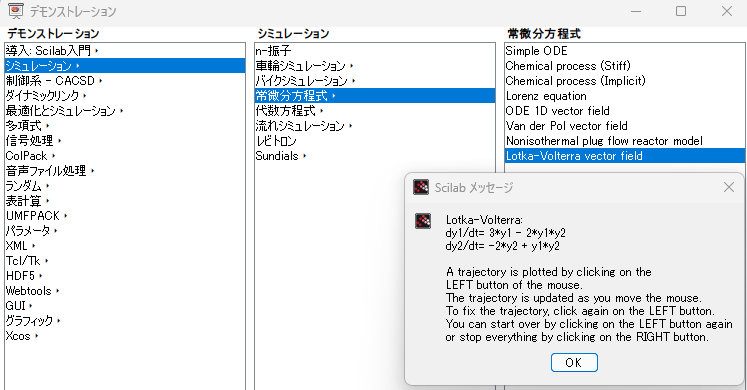
該当のソースファイルは以下です。
ode_ode_lotka.dem.sce
ここで登場するロットカ＝ヴォルテラ方程式も「シミュレーション業界じゃ、知らないとモグリ」的な方程式みたい。お惚け老人は、どこかで見た遠い記憶。ここでもGoogleの生成AI、Gemini 2.5 Flash様に解説をお願いしています。
ははん、「捕食者ー被食者モデル」ってやつだったのね。
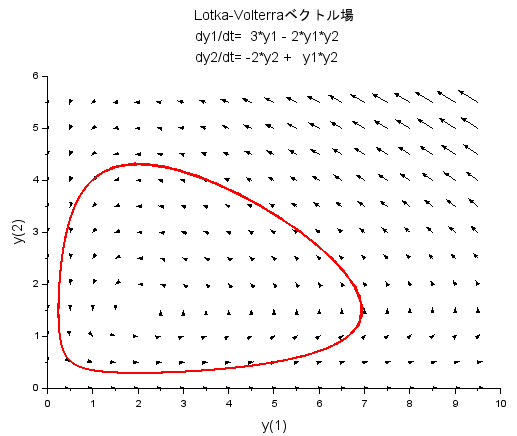
Scilabのデモスクリプトでは、y1がxの意味、y2がyの意味で良いかな。なお、この方程式の限界についてもGemini様はご指摘。
さて、プロットの実行結果が以下に。
横軸 y(1) が被食者の数、縦軸 y(2)が捕食者の数ってことでよかですかね。上記は適当な点を左クリックして現れた軌道ですが、捕食者が少ないところは急激に被食者増えてピークの７付近に到達、しかしその後捕食者の数も増えてきて被食者減少、捕食者の数４を超えたあたりで限界達したあと、急激に捕食者数が減り、元の木阿弥と。
どれも味わい深い方程式です。