「サイエンティフィックPythonのための」IDE、Spyder上にてScientific Python Lecturesの実習中。前回は線形計画法で老人の石頭をアップデート？今回はカーブフィッティングです。データ点に最も合うようにモデルとなる関数のパラメータを決定するもの。「非線形回帰」を練習してみます。
※「 ソフトな忘却力」投稿順 Index はこちら
※Scientific Python Lectures様のコースは例題だけでなく、エクササイズなども充実、それを全部順番に解いていったら必ずや立派な人になれるだろ～と思います。でも老い先短い年寄には量が多過ぎて多分死ぬまでに終わりません。適当な練習でお茶を濁してます。今回は「5.5 Optimization and fit: scipy.optimize」配下の「5.5.2 Curve Fitting」です。
scipy.optimize.curve_fit
レクチャでは、ありがちなCOS関数のパラメータをそのままCurve Fittingしてました。素直なCOSでノイズのようなものは乗せてません。実データは後のExerciseのお楽しみっという感じ。ううむ、ホンマモンの実データを使っていろいろ考察するのはメンドイです。そこで、以下の解説ページのExample（モデルとなる関数は指数関数）の関数をCOS関数に「差し替えて」乱数で実データの雰囲気をまとわせてカーブフィッティングしてみる妥協案。
Exampleを参考にしつつSpyder上で記述したスクリプトが以下に。
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
"""
Created on Fri Jun 20 14:15:43 2025
Curve Fitting sample
"""
import math
import numpy as np
import matplotlib.pyplot as plt
import scipy as sp
def fn(x, A, omega, theta):
return A * np.cos(omega * x + theta)
def main():
orgA = 0.5
orgOmega = 1.0
orgTheta = 0.1
org = (orgA, orgOmega, orgTheta)
xdata = np.linspace(0, 4 * math.pi, 50)
orgY = fn(xdata, orgA, orgOmega, orgTheta)
rng = np.random.default_rng()
ydata = orgY + 0.1 * rng.normal(size=xdata.size)
plt.scatter(xdata, ydata, s=2.0, color="blue", label="data w/Noise")
popt, pcov = sp.optimize.curve_fit(fn, xdata, ydata)
plt.plot(xdata, fn(xdata, orgA, orgOmega, orgTheta), 'r-', label='org: A=%5.3f, omega=%5.3f, theta=%5.3f' % tuple(org))
plt.plot(xdata, fn(xdata, *popt), 'g--', label='fit: A=%5.3f, omega=%5.3f, theta=%5.3f' % tuple(popt))
plt.xlabel('x')
plt.ylabel('y')
plt.legend(loc='lower right')
plt.show()
if __name__ == '__main__':
main()
オリジナルのモデル関数は、振幅A＝0.5、角速度ω＝1.0、位相θ=0.1の
\( A cos(\omega * x + \theta) \)
という形の余弦関数です。これに乱数（正規分布）をチョイと載せてやり、得た「ガタガタ」のデータ列（50点）に対して、Scipy.optimize.curve_fit関数を適用して、関数のA、ω、θを「フィット」していただこうという趣向です。
カーブフィッティングの結果
結果のグラフが以下に。
-
- 赤線はノイズの載ってないオリジナルの余弦波波形です。
- 青の点は上記の赤の関数上で50点(x, y)をとった上でyに誤差を載せたデータ点です。
- 緑の破線は、青の点列をCOS関数に対してカーブフィッティングして、A、ω、θを推定したもの
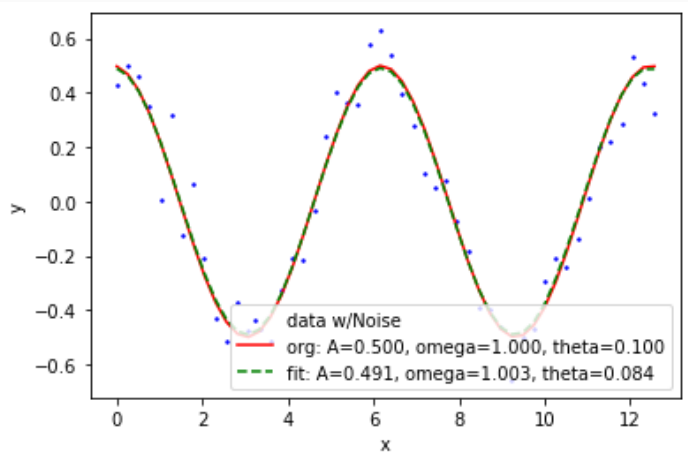上記の凡例に、オリジナルのA、ω、θとカーブフィッティングで求めたA、ω、θの推定値が並べてあります。結構イケてる？