「サイエンティフィックPythonのための」IDE、Spyder上にてScientific Python Lecturesの実習中。前回はカーブフィッティング。今回は関数の極小(あるいは極大)を求める算法です。見栄えがよいように2入力スカラー出力の関数の極小を探索してみたいと思います。当然「ひっかけ」な点もあり~の。
※「 ソフトな忘却力」投稿順 Index はこちら
※Scientific Python Lectures様のコースは例題だけでなく、エクササイズなども充実、それを全部順番に解いていったら必ずや立派な人になれるだろ~と思います。でも老い先短い年寄には量が多過ぎて多分死ぬまでに終わりません。適当な練習でお茶を濁してます。今回は「5.5 Optimization and fit: scipy.optimize」配下の「5.5.3 Optimization」です。
Optimization(最適化)問題
ある区間内で関数の最小値あるいは最大値を求めるOptimization問題は、アリガチすぎる問題かもしれませぬ。第94回の線形計画法などもその1種といってもいいかもしれませぬ。
SciPyは、線形に関わらず各種の関数をOptimazationできる関数を持っております。レクチャの「5.5.3 Optimization」では、まず1次元の関数を示して、Excersizeで2入力1出力の関数をやることになってました。まあね、1次元では簡単すぎる感じで見栄えがイマイチです。といってレクチャのExcersizeを真面目にやるのは遠慮したいヘタレの老人です。そこで思いついたのが、第88回で描いた「等高線図」です。そのときはカラーマップを変えて色変?を楽しみましたが、描いた等高線図には複数のピーク、複数の穴ぼこがあった記憶。今回はSciPyの関数を使ってその「等高線マップ」の穴の底(最小値)を見つけてみよう、ということであります。
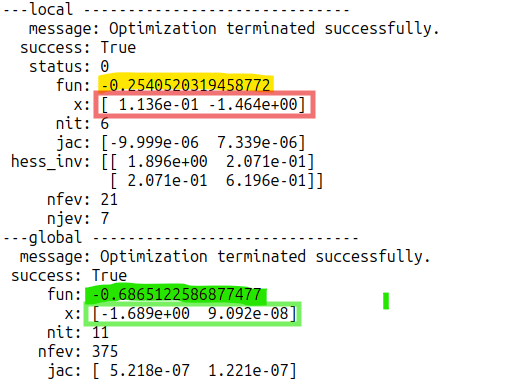
先に結果を示しておくとこんな感じ。「global minimizer」という方を使った場合は、しっかり「最小」を発見してます。しかし「local minimizer」を使った場合は、「意地悪な初期値 x0」を与えたせいで、局所的な穴ぼこにはまり込んでいる様子が見てとれます。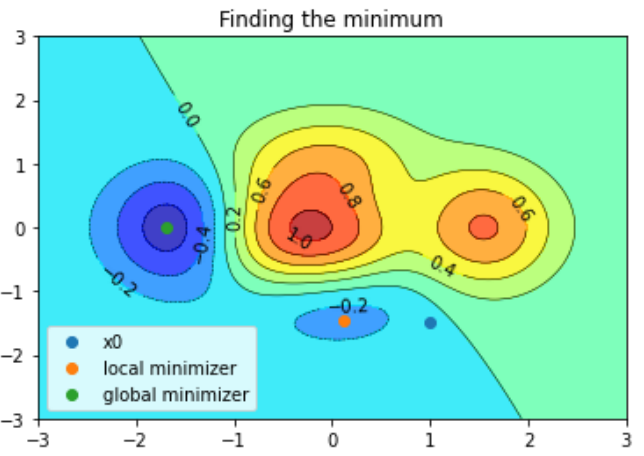
今回使用したスクリプトと適用アルゴリズム
レクチャのExampleを参考にしつつSpyder上で記述したスクリプトが以下に。
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
"""
Created on Sun Jun 22 2025
Finding the minimum (Optimization of a function)
"""
import numpy as np
import matplotlib.pyplot as plt
import scipy as sp
def f(x):
return (1 - x[0] / 2 + x[0]**5 + x[1]**3) * np.exp(-(x[0]**2) - x[1]**2)
def main():
n = 256
xlim = [-3, 3]
ylim = [-3, 3]
x = np.linspace(xlim[0], xlim[1], n)
y = np.linspace(ylim[0], ylim[1], n)
X, Y = np.meshgrid(x, y)
plt.contourf(X, Y, f([X, Y]), 8, alpha=0.75, cmap="jet")
C = plt.contour(X, Y, f([X, Y]), 8, colors="black", linewidths=0.5)
plt.clabel(C, inline=1, fontsize=10)
plt.title("Finding the minimum")
x0=[1, -1.5]
plt.scatter(x0[0], x0[1], label="x0")
res_local = sp.optimize.minimize(f, x0)
print("---local","---"*10, "\n", res_local)
plt.scatter(res_local.x[0], res_local.x[1], label="local minimizer")
res_global = sp.optimize.differential_evolution(f, bounds=[xlim, ylim])
print("---global","---"*10, "\n", res_global)
plt.scatter(res_global.x[0], res_global.x[1], label="global minimizer")
plt.legend(loc='lower left')
plt.show()
if __name__ == '__main__':
main()
コマケー話をメモっておくと、等高線図を描くときは、入力変数 x, y と与えていたfの引数ですが、最適化の場合は入力変数は1次元のベクトル1個であたえます。
上記の「local minimizer」で使用している関数のAPI解説ページが以下に
一方、「global minimizer」で使用している関数が以下に
scipy.optimize.differential_evolution
このような最適化問題で使われるアルゴリズムについて Googleの生成AI Gemini 2.5 Flash様に問いかけたらば、メッチャ沢山おしえてくれました。とても長くなるので、僭越ながら素人老人がまとめさせていただくと(AIに要約してもらうのではなく、老人がAIの出力を要約するという本末転倒)以下のごとし。
-
- 勾配ベースの方法 (Gradient-based Methods)
- 勾配フリーの方法 (Derivative-free Methods)
- 制約付き最適化 (Constrained Optimization)
うち、1番の勾配ベースの方法の中に
-
- 最急降下法 (Gradient Descent):
- 確率的勾配降下法 (Stochastic Gradient Descent, SGD)
- ニュートン法 (Newton’s Method)
- 準ニュートン法 (Quasi-Newton Methods)
などがあり、上記のminimize関数は、デフォルトで「準ニュートン法」に分類される、BFGS、L-BFGSといわれるようなアルゴリズムを「いい塩梅に見繕って」適用してくれるらしいです。
しかし、勾配ベースなので、局所的な穴ぼこに引っかかると抜け出せなくなる筈。まあ、今回も上記のサンプルコードでは、わざと意地悪な初期値を与えて(人間は等高線図みれば、どこにハマリそうかなど一目瞭然)わざわざそのようなケースを作ってみています。
一方、「global minimizer」で使用のdifferential_evolution関数は「勾配フリー」らしいです。Gemini 2.5 Flash様に教えていただいたアルゴズムの概要は以下のごとし。
おお、遺伝的アルゴリズム(進化計算?)の一種みたいね。素人老人は、訳も分からず大好きだなあ。GA。
Gemini様はアルゴリズムについていろいろ教えてくだすってますが、その辺飛ばして、利点を列挙しているところをとりだすとこんな感じ。
当然、GAベースの悪いところが見えることも無いとは言えんけれども、以下の説明など読むとかなりイイ感じなものみたい。知らんけど。
皆さん使っているのね~。ホントか?