「サイエンティフィックPythonのための」IDE、Spyder上にてScientific Python Lecturesの実習中。前回は確率分布３巨頭のお姿をグラフに描きました。今回は、ありがちな「平均」にもいろいろアリーノです。とはいえ算術平均ばかりが蔓延っていて、幾何平均や調和平均は若干影が薄い？そうなのか？
※「 ソフトな忘却力」投稿順 Index はこちら
※Scientific Python Lectures様のコースは例題だけでなく、エクササイズなども充実、それを全部順番に解いていったら必ずや立派な人になれるだろ～と思います。でも老い先短い年寄には量が多過ぎて多分死ぬまでに終わりません。適当な練習でお茶を濁してます。今回は「5.6 Statistics and random numbers: scipy.stats」配下の「5.6.2 Sample Statistics and Hypothesis Tests」です。
算術平均、幾何平均、調和平均
忘却力の老人の朧げな記憶によれば、平均をとる数列 a_i に対して、それぞれの要素のウエイトが全て同じ場合、３種類の平均は以下の式で計算できる筈。
算術平均
\( \frac {\sum_{i=1}^n a_i} {n} \)
幾何平均
\( \sqrt[n]{\prod_{i=1}^n a_i} \)
調和平均
\( \frac {n} {\sum_{i=1}^n \frac {1}{a_i}} \)
それぞれ用途によって使い分けよ、と言われるわけであります。
さて、numpyに算術平均を求める関数が含まれてますが、今回のSciPy.statsには、幾何平均、調和平均を求めるための関数どもが含まれてます。なお、SciPy.statsには、算術、幾何、調和の全ての上に君臨する？らしい power meanという関数もあるのですが、そいつは今回はパスということで。アリガチな３種類のみデス。
とりあえず３種類を計算
とりあえず NumPy と SciPy.stats の３種の「平均」関数をテキトーな人工データ（お惚け老人が気ままに手入力したもの）に対して適用してみました。処理はこんな感じ。
人工データ（２次元配列）をSpyderの変数ブラウザで眺めたものが以下に。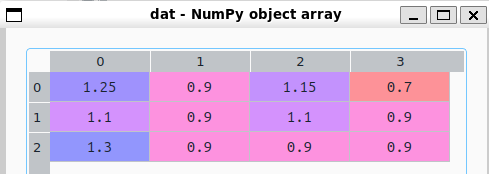
上記をみていただければ、一目瞭然かと思いますが、各行４データの算術平均は全て１になるように設えてあります。以下のmeanAをみてね。
また、各行の幾何平均はmeanG、調和平均はmeanHデス。平均関数実行後の変数の様子が以下に。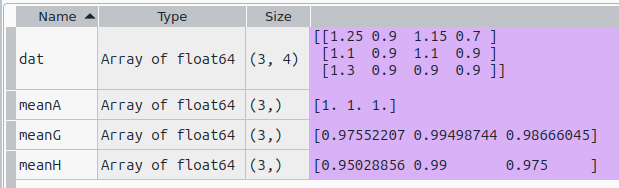
算術平均はオール1.0 だけれども、幾何平均や調和平均は違うね。当たり前か。
ただ上記の例では幾何平均や調和平均が「身に染みる」感じがしなかったので、それぞれ特有な例を計算してみました。
幾何平均
やっぱり銭こが絡むと記憶に残ります。ここでの計算例は株といたしましょう（初期投資をそのまま据え置いたとしてます。）ある年の運用成績はかなりよろしくて２０％アップ、その翌年も２０％の利益がでました。好調っす。しかし３年目、まさかの大暴落、資産は６０％に目減りデス。算術平均だと 1.2、1.2、0.6 で1.0で元の木阿弥に見えますが、そんなことはありませぬ。以下のように計算すると
datG = np.array([1.2, 1.2, 0.6]) datGav = sp.stats.gmean(datG)
その結果は、
datGavの値をご覧くだされ。
１をわりこんでおるな。でもこれは「３年間を平均したリターン」です。３年間のトータルではその値の３乗になるので、現時点での資産は元の86％あまりに減少してます。トホホ、あのとき売っておけばよかった、後の祭りよ。。。
調和平均
まあ、夏休みも近いです。新幹線のってどこかへ行ったと想像してください。移動速度は 300km/h とします。しかし、帰りは高速バスね。運賃、リーズナブルだし。移動速度は 100km/h とします。すると往復の平均速度は
datH = np.array([300, 100]) datHav = sp.stats.hmean(datH)
上記の計算結果が以下に。
datHavをご覧くだされ、150km/mが往復を均した平均速度です。単純に速度の算術平均とると 200km/h になってしまうのでおお間違いね。