「サイエンティフィックPythonのための」IDE、Spyder上にてScientific Python Lecturesの実習中。前回は平均でした。今回は数値積分です。SciPy.integrateには、各種の数値積分のツール群が備わってます。基本関数のお名前はQuad、またもや「知らないとモグリ」なライブラリ登場。
※「 ソフトな忘却力」投稿順 Index はこちら
※Scientific Python Lectures様のコースは例題だけでなく、エクササイズなども充実、それを全部順番に解いていったら必ずや立派な人になれるだろ～と思います。でも老い先短い年寄には量が多過ぎて多分死ぬまでに終わりません。適当な練習でお茶を濁してます。今回は「5.7 Numerical integration: scipy.integrate」配下の「5.7.1 Quadrature」です。
QUADPACKライブラリ
SciPy.integrate の中で数値積分を実行する一番基本的な関数のお名前は quad です。quadrature(数値積分）のquadをとっただけ？と思ったら、内部で
FORTRAN77の古典にして偉大なライブラリ、QUADPACK
を呼んでいるのでした。多分、直接QUADPACKを呼び出して使っているよゐこはあまり多くないと想像できるので、ほとんどの姉貴兄貴の皆さまはSciPyから呼び出しておるのではないかと。
簡単な数値積分をやってみる
APIの解説は以下にあります。
そこのExampleで x^2 を数値積分するという「いかにも」で「ベタな」例が上がっていたのでやってみます。
\( I1 = \int_{0}^{4} x^2 dx \)
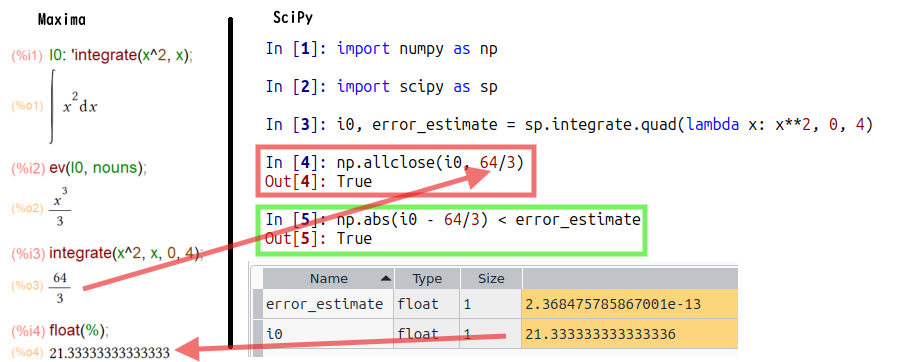
その前に、お手本。いつもお世話になっておりますフリーな数式処理系 Maxima様にお願いしてみます。Maxima様は数式処理系といってもお願いすれば浮動小数値を返してくれます。数値積分のパッケージもありますが、通常は、定積分してお答えを数値で求める形、人間と一緒っす。こんな感じ。
上記ではシンボル使って不定積分を行ってから、それとは無関係に定積分してます。定積分の結果は有理数 64/3 であると。それを無理やり浮動小数表現にしてます。
同じことをSciPyでやってみたのが以下に。
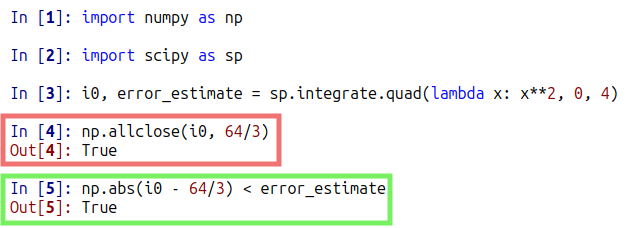
数値積分の結果が i0 に、誤差推定値が error_estimate に入っているので np.allclose関数とnp.abs関数で結果の正当性？を判定してます。まあ、Spyderの変数ブラウザ見れば一目瞭然だけれども。
ちょいと難し気な数値積分
ちょっと上の例は中学生？でもできそうだったので、もう少し込み入った例を計算してみます。最近やった以下の別件シリーズで
忘却の微分方程式(201)Maximaを使った物理数学基礎演習ノートを読む、ベッセル関数
「第１種ベッセル関数（νは整数でない）」を練習していたので、それをやってみたいと思います。SciPyの以下の解説ページに掲げられている例題そのものです。
数値積分する「第１種ベッセル関数（νは整数でない）」は以下です。
\( I1 = \int_{0}^{4.5} J_{2.5}(x) dx \)
SciPy上での数値積分は以下で
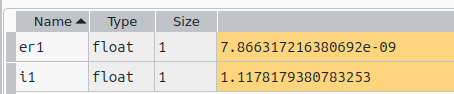
i1, er1 = sp.integrate.quad(lambda x: sp.special.jv(2.5,x), 0, 4.5)
その結果が以下です。
i1 あっているよな。多分。
重積分、無限も出てくるけどどうよ
お次は重積分です。まあ、SciPy的には重積分でも３重積分でもなんでもこいという感じなのですが、控えめに重積分ね。けれども積分範囲に無限も登場。大丈夫なのか？ 例題は以下の通り。
\( I2 = \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} e^{-(x^2+y^2)} dydx \)
SciPy上での数値積分は以下で
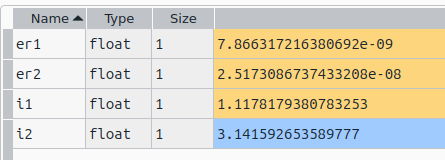
fun2 = lambda x, y: np.exp(-(x ** 2 + y ** 2)) i2, er2 = sp.integrate.dblquad(fun2, -np.inf, np.inf, -np.inf, np.inf)
その結果が以下です。
πが出てきたみたい。これでいいのか。まあ、処理例もそうなっているからいいか。