
「サイエンティフィックPythonのための」IDE、Spyder上にてScientific Python Lecturesの実習中。前回は数値積分、今回はODEの初期値問題です。SciPy.integrateで常微分方程式の数値解も一撃。題材は、最近別件シリーズで実習したばかりのLotka-Volterra方程式とな。
※「 ソフトな忘却力」投稿順 Index はこちら
※Scientific Python Lectures様のコースは例題だけでなく、エクササイズなども充実、それを全部順番に解いていったら必ずや立派な人になれるだろ~と思います。でも老い先短い年寄には量が多過ぎて多分死ぬまでに終わりません。適当な練習でお茶を濁してます。今回の「お勉強」は「5.7 Numerical integration: scipy.integrate」配下の「5.7.2 Initial Value Problems」です。
Lotka-Volterra方程式
何かいい(簡単わりに、やってます感のでる題材)ないかなと思って思いだしたのが以下です。
手習ひデジタル信号処理(189) Scilab、{Scilabデモ}、ODEの相平面解析?
つい1週間くらい前にやったばかりなので、忘却力の老人もぼんやり覚えてました。Lotka-Volterra方程式です。方程式の形が以下に。
\( \frac {dy_0}{dt} = \alpha \, y_0 \, – \, \beta \, y_0 \, y_1 \)
\( \frac {dy_1}{dt} = \delta \, y_0 \, y_1 \, – \, \gamma \, y_1 \)
有名な「捕食者」と「被食者」の関係を常微分方程式系でモデル化したアレです。上記のdy_0 が被食者の数(を表す数値)、dy_1 が捕食者の数(を表す数値)です。まさにSciPyの、solve_ivp()関数で解くにはバッチリな形。
Pythonによるモデル
上記の別シリーズ過去回ではScilab上でのScilabコードで表現されてましたが、今回はPythonです。それに過去回では「相平面」上での軌道を描くスタイルでしたが、今回はシンプルに捕食者、被食者の数の増減を時系列のグラフとしてます。なお、モデル中の、α、β、γ、δなどのパラメータは、過去回で使われている数値をそのままコピーさせていただきました。また、捕食者、被食者の数は整数ではなく、それに対応する「モデル上の」浮動小数点数値デス。
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
"""
Created on Sat Jun 28 2025
@author: jhalfmoon
Lotka-Volterra Equations
dy0/dt = alpha*y0 - beta*y0*y1
dy1/dt = delta*y0*y1 - gamma*y1
"""
import numpy as np
import matplotlib.pyplot as plt
import scipy as sp
def f(t, y, alpha, beta, delta, gamma):
""" Lotka-Volterra equations
"""
return (alpha*y[0] - beta*y[0]*y[1], delta*y[0]*y[1] - gamma*y[1])
def main():
alpha=3
beta=2
delta=1
gamma=2
t_span = (0, 10)
t_eval = np.linspace(*t_span, 100)
yinit = [4, 0.5]
res = sp.integrate.solve_ivp(
f, t_span, yinit, t_eval=t_eval,
args=(alpha, beta, delta, gamma), method='LSODA')
plt.plot(res.t, res.y[0], label="prey")
plt.plot(res.t, res.y[1], label="predator")
plt.title("Lotka-Volterra Equations")
plt.legend(loc='lower right')
plt.show()
if __name__ == '__main__':
main()
相平面上でのグラフを描くようになっていた過去回と比べると、単純グラフの今回は各段にシンプル。こんなんで良いのか?
実行結果
上記のPythonスクリプトを実行した結果のグラフが以下に。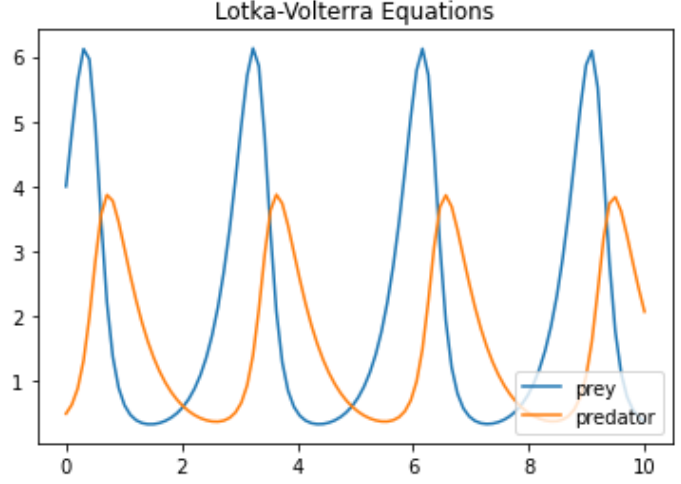
被食者(prey)が増えると、ちょと間をおいて捕食者(predator)が増加、すると被食者が激減、今度は捕食者も減というサイクルを繰り返します。
以下は過去回での相平面での様子のグラフ(再掲。初期値は似ているけど微妙に違う)です。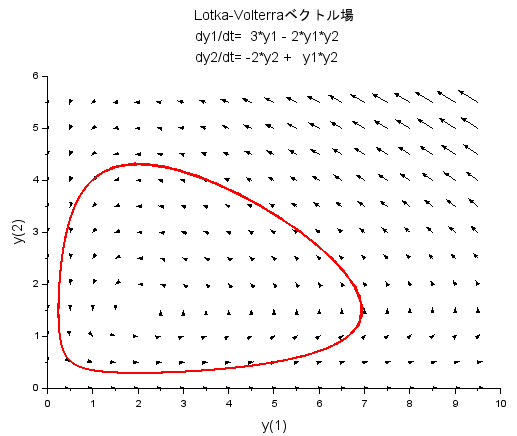
プレデターとか言うと恐ろし気なグラフにも見えるな。